2016-2017学年湖北省武汉市青山区七年级下学期期中数学试卷
试卷更新日期:2017-06-26 类型:期中考试
一、一.你一定能选对
-
1. 下列选项中能由左图平移得到的是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列所给数中,是无理数的是( )A、2 B、 C、0. D、3. 如图,小手盖住的点的坐标可能为( )
2. 下列所给数中,是无理数的是( )A、2 B、 C、0. D、3. 如图,小手盖住的点的坐标可能为( )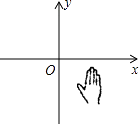 A、(﹣1,1) B、(﹣1,﹣1) C、(1,1) D、(1,﹣1)4. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )
A、(﹣1,1) B、(﹣1,﹣1) C、(1,1) D、(1,﹣1)4. 如图,直线AB、CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于( )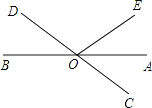 A、40° B、35° C、30° D、20°5. 点A(﹣3,﹣5)向右平移2个单位,再向下平移3个单位到点B,则点B的坐标为( )A、(﹣5,﹣8) B、(﹣5,﹣2) C、(﹣1,﹣8) D、(﹣1,﹣2)6. 下列各式正确的是( )A、 =±3 B、 =±4 C、 + =0 D、 ﹣ =17. 下列结论中:①若a=b,则 = ,②在同一平面内,若a⊥b,b∥c,则a⊥c;③直线外一点到直线的垂线段叫点到直线的距离;④| ﹣2|=2﹣ ,正确的个数有( )A、1个 B、2个 C、3个 D、4个8. 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )
A、40° B、35° C、30° D、20°5. 点A(﹣3,﹣5)向右平移2个单位,再向下平移3个单位到点B,则点B的坐标为( )A、(﹣5,﹣8) B、(﹣5,﹣2) C、(﹣1,﹣8) D、(﹣1,﹣2)6. 下列各式正确的是( )A、 =±3 B、 =±4 C、 + =0 D、 ﹣ =17. 下列结论中:①若a=b,则 = ,②在同一平面内,若a⊥b,b∥c,则a⊥c;③直线外一点到直线的垂线段叫点到直线的距离;④| ﹣2|=2﹣ ,正确的个数有( )A、1个 B、2个 C、3个 D、4个8. 如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠B=∠DCE;④AD∥BC且∠B=∠D.其中,能推出AB∥DC的是( )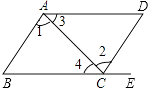 A、①④ B、②③ C、①③ D、①③④9. 如下表:被开方数a的小数点位置移动和它的算术平方根 的小数点位置移动规律符合一定的规律,若 =180,且﹣ =﹣1.8,则被开方数a的值为( )
A、①④ B、②③ C、①③ D、①③④9. 如下表:被开方数a的小数点位置移动和它的算术平方根 的小数点位置移动规律符合一定的规律,若 =180,且﹣ =﹣1.8,则被开方数a的值为( ).
…
0.000001
0.0001
0.01
1
100
10000
1000000
…
.
…
0.001
0.01
0.1
1
10
100
1000
…
A、32.4 B、324 C、32400 D、﹣324010. 如图,把一张对面互相平行的纸条折成如图所示那样,EF是折痕,若∠EFB=32°,则下列结论正确的有( )1)∠C′EF=32° (2) ∠AEC=116° (3)∠BGE=64° (4)∠BFD=116°.
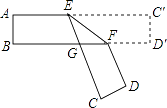 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、二.填空题
-
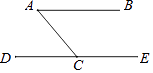
11. 计算:3 +2 = .12. 若点M(a﹣3,a+4)在x轴上,则a= .13. 如图,DE∥AB,若∠A=50°,则∠ACD= .
 14. 如图,以数轴的单位长度线段为边长作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是 .
14. 如图,以数轴的单位长度线段为边长作一个正方形,以表示数2的点为圆心,正方形对角线长为半径画半圆,交数轴于点A和点B,则点A表示的数是 .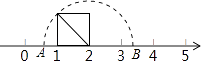 15. 已知AB∥x轴,且AB=3,若点A的坐标是(﹣1,2),则B点的坐标是 .16. 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转°.
15. 已知AB∥x轴,且AB=3,若点A的坐标是(﹣1,2),则B点的坐标是 .16. 如图,小明从A出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C处,此时需把方向调整到与出发时一致,则方向的调整应是右转°.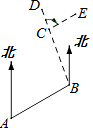
三、三.解下列各题
-
17. 求下列各式的值:(1)、x2﹣25=0(2)、x3﹣3= .18. 如图,在三角形ABC中,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°,∠AED=40°;
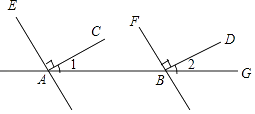
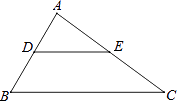 (1)、求证:DE∥BC;(2)、求∠C的度数.19. 看图填空,并在括号内注明理由依据,
(1)、求证:DE∥BC;(2)、求∠C的度数.19. 看图填空,并在括号内注明理由依据,解:∵∠1=30°,∠2=30°
∴∠1=∠2
∴∥()
又AC⊥AE(已知)
∴∠EAC=90°
∴∠EAB=∠EAC+∠1=120°
同理:∠FBG=∠FBD+∠2=°.
∴∠EAB=∠FBG().
∴∥(同位角相等,两直线平行)
 20. 如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点.
20. 如图,在边长为1的小正方形组成的网格中,A、B、C、D、E五点都是格点. (1)、请在网格中建立合适的平面直角坐标系,使点A、B两点坐标分别是A(﹣3,0)、B(2,﹣1);(2)、在(1)条件下,请直接写出C、D、E三点的坐标;(3)、则三角形BDE的面积为21. 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)、请帮小丽设计一种可行的裁剪方案;(2)、若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案;若不能,请简要说明理由.22. 如图,已知∠A=∠AGE,∠D=∠DGC.
(1)、请在网格中建立合适的平面直角坐标系,使点A、B两点坐标分别是A(﹣3,0)、B(2,﹣1);(2)、在(1)条件下,请直接写出C、D、E三点的坐标;(3)、则三角形BDE的面积为21. 小丽想用一块面积为400cm2的正方形纸片,沿着边的方向裁处一块面积为300cm2的长方形纸片.(1)、请帮小丽设计一种可行的裁剪方案;(2)、若使长方形的长宽之比为3:2,小丽能用这块纸片裁处符合要求的纸片吗?若能,请帮小丽设计一种裁剪方案;若不能,请简要说明理由.22. 如图,已知∠A=∠AGE,∠D=∠DGC.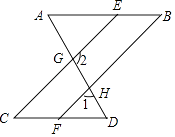 (1)、求证:AB∥CD;(2)、若∠2+∠1=180°,且∠BEC=2∠B+30°,求∠C的度数.23. 如图1,已知AB∥CD,∠B=30°,∠D=120°;
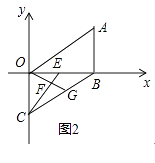
(1)、求证:AB∥CD;(2)、若∠2+∠1=180°,且∠BEC=2∠B+30°,求∠C的度数.23. 如图1,已知AB∥CD,∠B=30°,∠D=120°;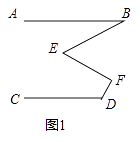 (1)、若∠E=60°,则∠F=;(2)、请探索∠E与∠F之间满足的数量关系?说明理由;(3)、如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.
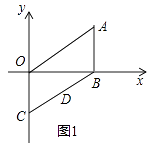
(1)、若∠E=60°,则∠F=;(2)、请探索∠E与∠F之间满足的数量关系?说明理由;(3)、如图2,已知EP平分∠BEF,FG平分∠EFD,反向延长FG交EP于点P,求∠P的度数.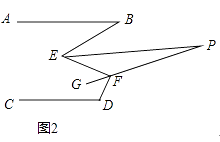 24. 已知,在平面直角坐标系中,AB⊥x轴于点B,点A(a,b)满足 +|b﹣2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.(1)、则a= , b=;点C坐标为;(2)、
24. 已知,在平面直角坐标系中,AB⊥x轴于点B,点A(a,b)满足 +|b﹣2|=0,平移线段AB使点A与原点重合,点B的对应点为点C.(1)、则a= , b=;点C坐标为;(2)、如图1,点D(m,n)在线段BC上,求m、n满足的关系式;
 (3)、
(3)、如图2,E是线段OB上一动点,以OB为边作∠BOG=∠AOB,交BC于点G,连CE交OG于点F,当点E在线段OB上运动过程中, 的值是否会发生变化?若变化请说明理由,若不变,请求出其值.