2017年山东省青岛市黄岛区中考数学一模试卷

试卷更新日期：2017-06-26 类型：中考模拟

进入出卷网下载

一、选择题

1. ﹣ $\frac{1}{2}$ 的绝对值是（）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、2 D、﹣2

查看试题解析
2. 国家卫生和计划生育委员会公布H7N9禽流感病毒直径约为0.0000001m，则病毒直径0.0000001m用科学记数法表示为（）（保留两位有效数字）．

A、0.10×10^﹣⁶m B、1×10^﹣⁷m C、1.0×10^﹣⁷m D、0.1×10^﹣⁶m

查看试题解析
3. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算不正确的是（　　）

A、a³•a²=a⁵ B、（x³）²=x⁹ C、x⁵+x⁵=2x⁵ D、（﹣ab）⁵÷（﹣ab）²=﹣a³b³

查看试题解析
5. 如图是由6个相同的小正方体搭成的几何体，那么这个几何体的俯视图是（）

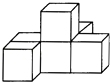A、 B、 C、 D、

查看试题解析
6.
为了锻炼学生身体素质，训练定向越野技能，某校在一公园内举行定向越野挑战赛．路线图如图1所示，点E为矩形ABCD边AD的中点，在矩形ABCD的四个顶点处都有定位仪，可监测运动员的越野进程，其中一位运动员P从点B出发，沿着B﹣E﹣D的路线匀速行进，到达点D．设运动员P的运动时间为t，到监测点的距离为y．现有y与t的函数关系的图象大致如图2所示，则这一信息的来源监测点为（）

A、A点 B、B点 C、C点 D、D点

查看试题解析
7. 如图，四边形ABCD是⊙O的内接四边形，∠B=135°，则∠AOC的度数为（）

A、45° B、90° C、100° D、135°

查看试题解析
8. 函数y= $\frac{k}{x}$ 与y=kx²﹣k（k≠0）在同一直角坐标系中的图象可能是（）

A、 B、 C、 D、

查看试题解析

二、填空题

9. 计算： $\frac{\sqrt{48} - \sqrt{27}}{\sqrt{12}}$ = ．

查看试题解析
10. 一个不透明的袋子中装有15个黑球，若干个白球，这些球除颜色不同外，其余均相同，若从中随机摸出一个球是白球的概率是 $\frac{2}{5}$ ，则袋子中的白球有个．

查看试题解析
11. 汛期来临之前，某地要对辖区内的4600米河堤进行加固．施工单位在加固800米后，采用新的加固模式，这样每天加固长度是原来的2倍，结果仅用10天便出色完成了全部任务．请求出施工单位原来每天加固河堤多少米？设原来每天加固河堤x米，根据题意可得方程．

查看试题解析
12. 如图，在△ABC中，OA=OB=6，∠O=120°，以点O为圆心的⊙O和底边AB相切于点C，则阴影部分的面积为．

查看试题解析
13. 如图，在正方形ABCD中，O是对角线的交点，过点O作OE⊥OF，分别交AD，CD于E，F，若AE=6，CF=4，则EF= ．

查看试题解析
14. 如图放置的△OAB₁ ， △B₁A₁B₂ ， △B₂A₂B₃ ， …都是边长为2的等边三角形，点A在x轴上，点O，B₁ ， B₂ ， B₃ ， …都在正比例函数y=kx的图象l上，则点B₂₀₁₇的坐标是．

查看试题解析

三、作图题

15. 已知：如图，线段a，∠α．
求作：Rt△ABC，使∠C=90°，∠A=∠α，AC=a．

查看试题解析

四、解答题

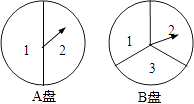
16. 计算下列各题

(1)、化简：（ $\frac{1}{x + 2}$ ﹣1）÷ $\frac{1 - x^{2}}{x + 2}$

(2)、关于x的一元二次方程kx²+2x﹣3=0有两个不相等的实数根，求k的取值范围．

查看试题解析
17. 小明和小亮用下面两个可以自由转动的转盘做游戏，每个转盘被分成面积相等的几个扇形．转动两个转盘各一次，若两次数字之积大于2，则小明胜，否则小亮胜．这个游戏对双方公平吗？请说明理由．

查看试题解析
18. 随着全国各地空气出现严重污染，PM2.5屡屡爆表，我国多个城市发生雾霾天气，越来越多的人开始关注一个原本陌生的术语﹣PM2.5．某校九年级共有1000名学生，团委准备调查他们对“PM2.5”知识的了解程度．

(1)、在确定调查方式时，团委设计了以下三种方案：
方案一：调查九年级部分女生；
方案二：调查九年级部分男生；
方案三：到九年级每个班去随机调查一定数量的学生．
请问其中最具有代表性的一个方案是；

(2)、团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图，请你根据图中信息，将其补充完整；

(3)、请你估计该校九年级约有多少名学生比较了解“PM2.5”的知识．

查看试题解析
19.
在某次反潜演习中，红方军舰A测得蓝方潜艇C的俯角为31°，位于军舰A正上方800米的红方反潜直升机B测得潜艇C的俯角为65°．试根据以上数据求出潜艇C离开海平面的下潜深度（结果保留整数）
（参考数据：sin31°≈ $\frac{1}{2}$ ，tan31°≈ $\frac{3}{5}$ ，sin65°≈ $\frac{9}{10}$ ，tan65°≈ $\frac{15}{7}$ ）

查看试题解析
20. 某市在一次市政施工中，有两段长度相等的人行道铺设任务，分别交给甲、乙两个施工队同时进行施工．如图是反映所铺设人行道的长度y（米）与施工时间x（时）之间关系的部分图象．请解答下列问题：

(1)、求乙队在2≤x≤6的时间段内，y与x的函数关系式；

(2)、若甲队施工速度不变，乙队在施工6小时后，施工速度增加到12米/时，结果两队同时完成了任务．求甲队从开始施工到完成，所铺设的人行道共是多少米？

查看试题解析
21. 如图，茬四边形ABCD中，AD∥BC，E是BC的中点，AC平分∠BCD，且AC⊥AB，接DE，交AC于F．

(1)、求证：AD=CE；

(2)、若∠B=60°，试确定四边形ABED是什么特殊四边形？请说明理由．

查看试题解析
22. 某商场经营某种品牌的玩具，购进的单价是30元，根据市场调查：在一段时间内，销售单价是40元时，销售量是600件，而销售单价每涨1元，就会少售出10件玩具，

(1)、设该种品牌玩具的销售单价为x元，请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元；

(2)、在（1）问条件下，若商场获得了10000元销售利润，求该玩具销售单价x应定为多少元？

(3)、在（1）问条件下，若玩具厂规定该品牌玩具销售单价不低于45元，且商场要完成不少于480件的销售任务，求商场销售该品牌玩具获得的最大利润是多少？

查看试题解析

23.

问题提出：用水平线和竖直线将平面分成若干个面积为1的小长方形格子，小长方形的顶点叫格点，以格点为顶点的多边形叫格点多边形．设格点多边形的面积为S，它各边上格点的个数和为x，多边形内部的格点数为n，S与x，n之间是否存在一定的数量关系呢？

(1)、问题探究：

如图1，图中所示的格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数和的对应关系如下表，请填写下表并写出S与x之间的关系式S= ．

多边形的序号	①	②	③	④	…
多边形的面积S	2	2.5	3	4	…
各边上格点的个数和x	4				…

(2)、在图2中所示的格点多边形，这些多边形内部都有且只有2个格点．探究此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S= ．

(3)、请继续探索，当格点多边形内部有且只有n（n是正整数）个格点时，猜想S与x，n之间的关系式S=（用含有字母x，n的代数式表示）

(4)、问题拓展：

请在正三角形网格中的类似问题进行探究：在图3、4中正三角形网格中每个小正三角形面积为1，小正三角形的顶点为格点，以格点为顶点的多边形称为格点多边形，图是该正三角形格点中的两个多边形．

根据图中提供的信息填表：

	格点多边形各边上的格点的个数	格点多边形内部的格点个数	格点多边形的面积
多边形1（图3）	8	1	8
多边形2（图4）	7	3	11
…	…	…	…
…	…	…	…
…	…	…	…
一般格点多边形	a	b	S

则S与a，b之间的关系为S=（用含a，b的代数式表示）．

查看试题解析

24.
已知：如图，在Rt△ABC中，∠C=90°，AC=3cm，BC=4cm，点P从点B出发，沿BC向点C匀速运动，速度为1cm/s；过点P作PD∥AB，交AC于点D，同时，点Q从点A出发，沿AB向点B匀速运动，速度为2cm/s；当一个点停止运动时，另一个点也停止运动，连接PQ．设运动时间为t（s）（0＜t＜2.5），解答下列问题：

(1)、当t为何值时，四边形ADPQ为平行四边形？

(2)、设四边形ADPQ的面积为y（cm²），试确定y与t的函数关系式；

(3)、在运动过程中，是否存在某一时刻t，使S_四边形_ADPQ：S_△_PQB=13：2？若存在，请说明理由，若存在，求出t的值，并求出此时PQ的距离．

查看试题解析