2017年山东省临沂市兰山区中考数学模拟试卷(4月份)
试卷更新日期:2017-06-26 类型:中考模拟
一、选择题
-
1. ﹣2的倒数是( )A、2 B、 C、﹣ D、﹣0.22. 如图,BC⊥AE于点C,CD∥AB,∠B=55°,则∠1等于( )
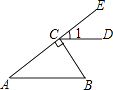 A、35° B、45° C、55° D、65°3. 下列计算中,正确的是( )A、2a+3b=5ab B、(3a3)2=6a6 C、a6+a2=a3 D、﹣3a+2a=﹣a4. 不等式 的解集在数轴上表示正确的是( )A、
A、35° B、45° C、55° D、65°3. 下列计算中,正确的是( )A、2a+3b=5ab B、(3a3)2=6a6 C、a6+a2=a3 D、﹣3a+2a=﹣a4. 不等式 的解集在数轴上表示正确的是( )A、 B、
B、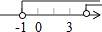 C、
C、 D、
D、 5. 如图,组合体的俯视图是( )
5. 如图,组合体的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 6. 一个布袋内只装有1个黑球和2个白球,这些球除颜色外其余都相同,随机摸出一个球后放回并搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )A、 B、 C、 D、7. 一个多边形的内角和是外角和的2倍,这个多边形的边数为( )A、5 B、6 C、7 D、88. 将一块矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好围成一个容积为15m3的无盖长方体水箱,且此长方体水箱的底面长比宽多2米.求该矩形铁皮的长和宽各是多少米?若设该矩形铁皮的宽是x米,则根据题意可得方程为( )A、(x+2)(x﹣2)×1=15 B、x(x﹣2)×1=15 C、x(x+2)×1=15 D、(x+4)(x﹣2)×1=159. 小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )A、255分 B、84分 C、84.5分 D、86分10. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )
6. 一个布袋内只装有1个黑球和2个白球,这些球除颜色外其余都相同,随机摸出一个球后放回并搅匀,再随机摸出一个球,则两次摸出的球都是黑球的概率是( )A、 B、 C、 D、7. 一个多边形的内角和是外角和的2倍,这个多边形的边数为( )A、5 B、6 C、7 D、88. 将一块矩形铁皮的四个角各剪去一个边长为1米的正方形后,剩下的部分刚好围成一个容积为15m3的无盖长方体水箱,且此长方体水箱的底面长比宽多2米.求该矩形铁皮的长和宽各是多少米?若设该矩形铁皮的宽是x米,则根据题意可得方程为( )A、(x+2)(x﹣2)×1=15 B、x(x﹣2)×1=15 C、x(x+2)×1=15 D、(x+4)(x﹣2)×1=159. 小王参加某企业招聘测试,他的笔试、面试、技能操作得分分别为85分、80分、90分,若依次按照2:3:5的比例确定成绩,则小王的成绩是( )A、255分 B、84分 C、84.5分 D、86分10. 如图,线段AB是⊙O的直径,弦CD丄AB,∠CAB=20°,则∠AOD等于( )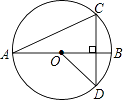 A、160° B、150° C、140° D、120°11. 一组按规律排列的式子:a2 , , , ,…,则第2017个式子是( )A、 B、 C、 D、12. 如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )
A、160° B、150° C、140° D、120°11. 一组按规律排列的式子:a2 , , , ,…,则第2017个式子是( )A、 B、 C、 D、12. 如图,△ABC为等边三角形,P为BC上一点,△APQ为等边三角形,PQ与AC相交于点M,则下列结论中正确的是( )①AB∥CQ;②∠ACQ=60°;③AP2=AM•AC;④若BP=PC,则PQ⊥AC.
 A、①② B、①③ C、①②③ D、①②③④13. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( )
A、①② B、①③ C、①②③ D、①②③④13. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①2a+b<0;②abc>0;③4a﹣2b+c>0;④a+c>0,其中正确结论的个数为( ) A、4个 B、3个 C、2个 D、1个14. 如图,直线y=kx与双曲线y=﹣ 交于A(x1 , y1),B(x2 , y2)两点,则2x1y2﹣8x2y1的值为( )
A、4个 B、3个 C、2个 D、1个14. 如图,直线y=kx与双曲线y=﹣ 交于A(x1 , y1),B(x2 , y2)两点,则2x1y2﹣8x2y1的值为( ) A、﹣6 B、﹣12 C、6 D、12
A、﹣6 B、﹣12 C、6 D、12二、填空题
-
15. 分解因式:m3n﹣4mn= .16. 计算(a﹣ )÷ 的结果是 .17. 如图,▱ABCD的周长为36,对角线AC,BD相交于点O.点E是CD的中点,BD=12,则△DOE的周长为 .
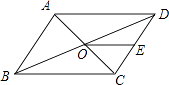 18. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD= ,则△ABC的面积为 .
18. 如图,在△ABC中,∠C=90°,AC=2,点D在BC上,∠ADC=2∠B,AD= ,则△ABC的面积为 . 19. 数的概念是从实践中产生和发展起来的,在学习了实数以后,像x2=﹣1这样的方程还是没有实数解的,因为没有一个实数的平方等于﹣1,即负数在实数范围内没有平方根,所以为了了解形如x2=﹣1这类方程的解,就要引入一个新的数i.定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.在这种情况下,i可以与实数b相乘再同实数a相加从而得到形如“a+bi”(a、b为实数)的数,人们把这种数叫作复数,a叫这个复数的实部,b叫做这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.比如:(2+i)+(5﹣3i)=(2+5)+(1﹣3)i=7﹣2i.请你根据对以上内容的理解,计算:(3+i)(3﹣i)= .
19. 数的概念是从实践中产生和发展起来的,在学习了实数以后,像x2=﹣1这样的方程还是没有实数解的,因为没有一个实数的平方等于﹣1,即负数在实数范围内没有平方根,所以为了了解形如x2=﹣1这类方程的解,就要引入一个新的数i.定义:如果一个数的平方等于﹣1,记为i2=﹣1,这个数i叫做虚数单位.在这种情况下,i可以与实数b相乘再同实数a相加从而得到形如“a+bi”(a、b为实数)的数,人们把这种数叫作复数,a叫这个复数的实部,b叫做这个复数的虚部.它的加、减、乘法运算与整式的加、减、乘法运算类似.比如:(2+i)+(5﹣3i)=(2+5)+(1﹣3)i=7﹣2i.请你根据对以上内容的理解,计算:(3+i)(3﹣i)= .三、解答题
-
20. 计算:( )﹣1﹣(π﹣3.14)0﹣ +2sin60°.21. 为配合全市“禁止焚烧秸秆”工作,某学校举行了“禁止焚烧秸秆,保护环境,从我做起”为主题的演讲比赛.赛后组委会整理参赛同学的成绩,并制作了如下不完整的频数分布表和频数分布直方图.
分数段(分数为x分)
频数
百分比
60≤x<70
8
20%
70≤x<80
a
30%
80≤x≤90
16
b%
90≤x<100
4
10%
请根据图表提供的信息,解答下列问题:
(1)、表中的a= , b=;请补全频数分布直方图;(2)、若用扇形统计图来描述成绩分布情况,则分数段70≤x<80对应扇形的圆心角的度数是多少? 22. 如图,一辆汽车从P处出发,先沿北偏东60°的方向行驶到达A处后,接着向正南方向行驶100( +1)千米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少千米?
22. 如图,一辆汽车从P处出发,先沿北偏东60°的方向行驶到达A处后,接着向正南方向行驶100( +1)千米到达B处.在B处观测到出发时所在的P处在北偏西45°方向上,P,A两处相距多少千米?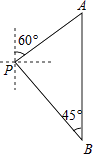 23. 如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.
23. 如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.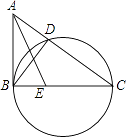 (1)、求证:AB是圆的切线;(2)、若点E是BC上一点,已知BE=4,tan∠AEB= ,AB:BC=2:3,求圆的直径.24. “世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.某车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%.(A、B两种型号车今年的进货和销售价格如下表所示)
(1)、求证:AB是圆的切线;(2)、若点E是BC上一点,已知BE=4,tan∠AEB= ,AB:BC=2:3,求圆的直径.24. “世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.某车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%.(A、B两种型号车今年的进货和销售价格如下表所示)A型车
B型车
进货价格(元/辆)
1100
1400
销售价格(元/辆)
今年的销售价格
2400
(1)、求今年4月份A型车每辆销售价多少元(用列方程进行解答);(2)、该车行计划5月份新进一批A型车和B型车共50辆,设购进的A型车为x辆,获得的总利润为y元,请写出y与x之间的函数关系式;(3)、在(2)的条件下,若B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最大?最大利润是多少?25. 已知在菱形ABCD中,∠ABC=60°,对角线AC、BD相交于点O,点E是线段BD上一动点(不与点B,D重合),连接AE,以AE为边在AE的右侧作菱形AEFG,且∠AEF=60°.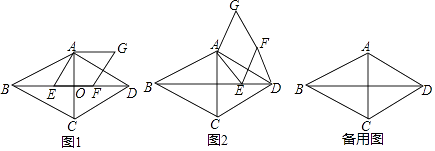 (1)、如图1,若点F落在线段BD上,请判断:线段EF与线段DF的数量关系是.(2)、如图2,
(1)、如图1,若点F落在线段BD上,请判断:线段EF与线段DF的数量关系是.(2)、如图2,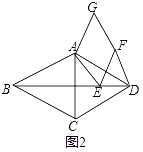
若点F不在线段BD上,其它条件不变,(1)中的结论是否仍然成立?请给出判断并予以证明;
(3)、若点C,E,G三点在同一直线上,其它条件不变,请直接写出线段BE与线段BD的数系.26. 如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l,交抛物线于点Q.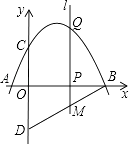 (1)、求抛物线的解析式;(2)、求直线BD的解析式;(3)、当点P在线段OB上运动时,直线l交BD于点M,是否存在点P,使得四边形CQMD是平行四边形?若存在,求出m的值;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、求直线BD的解析式;(3)、当点P在线段OB上运动时,直线l交BD于点M,是否存在点P,使得四边形CQMD是平行四边形?若存在,求出m的值;若不存在,请说明理由.