2017年山东省济宁市微山县中考数学一模试卷
试卷更新日期:2017-06-26 类型:中考模拟
一、选择题
-
1. 2017的倒数是( )A、 B、﹣2017 C、2017 D、2. 下列各式成立的是( )A、2x﹣x=2 B、(x3)3=x6 C、|π﹣2 |=2 ﹣π D、x2÷x3=x3. 在落实“小组合作学习,当堂达标检测及评价”要求中,某班四个小组设计的组徽图案如图,这四个图案中,既是轴对称图形又是中心对称图形的是( )A、
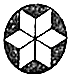 B、
B、 C、
C、 D、
D、 4. 李克强总理在2017年政府工作报告中指出:“完善就业政策,加大就业培训力度,加强对灵活就业、新就业形态的支持,今年高校毕业生7950000人,再创历史新高,要实施好就业促进、创业引领、基层成长等计划,促进多渠道就业创业.”其中数据7950000用科学记数法表示是( )A、795×104 B、7.95×105 C、0.795×107 D、7.95×1065. 如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )
4. 李克强总理在2017年政府工作报告中指出:“完善就业政策,加大就业培训力度,加强对灵活就业、新就业形态的支持,今年高校毕业生7950000人,再创历史新高,要实施好就业促进、创业引领、基层成长等计划,促进多渠道就业创业.”其中数据7950000用科学记数法表示是( )A、795×104 B、7.95×105 C、0.795×107 D、7.95×1065. 如图,平行四边形ABCD的对角线AC,BD相交于点O,补充下面一个条件,不能判定平行四边形ABCD是菱形的是( )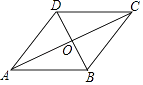 A、AB=BC B、AO=BO C、∠DOC=90° D、∠CDO=∠ADO6. 化简 ﹣ 的结果等于为( )A、﹣a﹣2 B、﹣ C、 D、7.
A、AB=BC B、AO=BO C、∠DOC=90° D、∠CDO=∠ADO6. 化简 ﹣ 的结果等于为( )A、﹣a﹣2 B、﹣ C、 D、7.已知:正方体展开图(如图所示)相对面上的数值相等,那么x的值等于( )
 A、﹣1 B、a﹣2 C、﹣1或2 D、1或﹣28. 如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为 m,弦CD=4m,那么隧道的最高处到CD的距离是( )
A、﹣1 B、a﹣2 C、﹣1或2 D、1或﹣28. 如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为 m,弦CD=4m,那么隧道的最高处到CD的距离是( )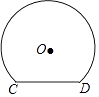 A、 m B、4m C、 m D、6m9. 如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y= 在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1 , y1)和点(x2 , y2)在反比例函数的图象上,若x1>x2 , 则y1<y2;③不等式x+2< 的解集是0<x<1.其中正确的有( )
A、 m B、4m C、 m D、6m9. 如图,在平面直角坐标系中,直线y=x+2与x轴交于点A,与y轴交于点C,与反比例函数y= 在第一象限内的图象交于点B(1,3),连接BO,下面三个结论:①S△AOB=1.5,;②点(x1 , y1)和点(x2 , y2)在反比例函数的图象上,若x1>x2 , 则y1<y2;③不等式x+2< 的解集是0<x<1.其中正确的有( ) A、0个 B、1个 C、2个 D、3个10. 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )
A、0个 B、1个 C、2个 D、3个10. 如图,把正六边形各边按同一方向延长,使延长的线段与原正六边形的边长相等,顺次连接这六条线段外端点可以得到一个新的正六边形,…,重复上述过程,经过2018次后,所得到的正六边形边长是原正六边形边长的( )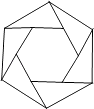 A、( )2016倍 B、( )2017倍 C、( )2018倍 D、( )2019倍
A、( )2016倍 B、( )2017倍 C、( )2018倍 D、( )2019倍二、填空题
-
11. 一天,小明读一本数学课外书,他从m页读到n页,他共读了页.12. 已知正比例函数y=kx(k为常数,且k≠0)的图象经过第二、四象限,则k的值可以是 . (写出一个即可)
13. 如图,从一个直径是2m的圆形铁皮中剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,那么圆锥的高等于 . 14. 为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
14. 为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是 .
15. 如图,点D是等边△ABC内一点,DA=8,BD=10,CD=6,则∠ADC的度数是 .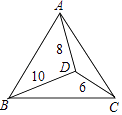
三、解答题
-
16. 解不等式组 并在数轴上表示出它的解集.17. 已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角.
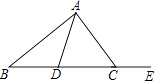 (1)、读下列语句,尺规作图,保留作图痕迹.
(1)、读下列语句,尺规作图,保留作图痕迹.①作∠ACE的角平分线,交BA延长线于点F;
②过点D作DH∥AC,交AB于点H,连接CH.
(2)、依据以上条件,解答下列问题.①与△AHD面积相等的三角形是;
②若∠B=40°,∠F=30°,求∠BAC的度数.
18. 2017年3月23日,在世界杯预赛亚洲区12强赛A组6轮的较量中,中国足球队以1﹣0的比分战胜老对手韩国队晋级12强.某初中学校为了了解本校800名学生对本次比赛的关注程度,以便做好引导和教育工作,随机抽取了150名学生进行调查,按年级人数和关注程度,分别绘制了条形统计图(图1)和扇形统计图(图2).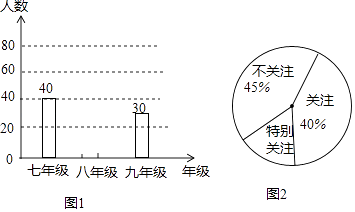 (1)、请你补全条形统计图,并求“特别关注”所在扇形的圆心角的度数;(2)、求全校不关注本场比赛的学生大约有多少名?(3)、在这次调查中
(1)、请你补全条形统计图,并求“特别关注”所在扇形的圆心角的度数;(2)、求全校不关注本场比赛的学生大约有多少名?(3)、在这次调查中, 九年级共有两位男生和两位女生“不关注”本次比赛,现准备从四人中随机抽取两人进行座谈,请用列表法或画树状图的方法求出抽取的两人恰好是一男生和一女生的概率.
19. 2016年12月28日举行了微山县南阳镇北、两城镇南跨湖高速的路线开工仪式,其中的一项工程由A、B两工程队合作,120天可以完成;如果A,B两工程队单独完成此项工程,B工程队所用时间是A工程队的1.5倍.(1)、求A,B两工程队单独完成此项工程各需多少天?(2)、在施工过程中,该总公司派一名技术人员在现场对施工质量进行全程监督,每天总公司补助技术人员100元,若由A工程队单独施工,平均每天A工程队的费用为0.5万元,现总公司选择了B工程队单独施工,要求总费用不能超过选择A工程队时的总费用,则平均每天B工程队的费用最多为多少?20. 如图,点E为矩形ABCD的边BC的中点,以DE为直径的⊙O交AD于H点,过点H作HF⊥AE于点F.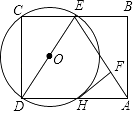 (1)、求证:HF是⊙O的切线;(2)、若DH=3,AF=2,求⊙O的半径.21. 【阅读新知】
(1)、求证:HF是⊙O的切线;(2)、若DH=3,AF=2,求⊙O的半径.21. 【阅读新知】三角形中任何一边的平方等于其它两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
即:如图1,.
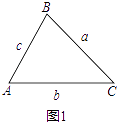
在△ABC中,已知AB=c,BC=a,CA=b,则有:
a2=b2+c2﹣2bccosA,b2=a2+c2﹣2accosB,c2=a2+b2﹣2abcosC
利用这个正确结论可求解下列问题:
例在△ABC中,已知a=2 ,b=2 ,c= ,求∠A.
解:∵a2=b2+c2﹣2bccosA,
cosA= = = .
∴∠A=60°.
【应用新知】
(1)、选择题:在△ABC中,已知b=ccosA,a=csinB,那么△ABC是( ).A、等边三角形 B、等腰三角形 C、等腰直角三角形 D、直角三角形(2)、如图2,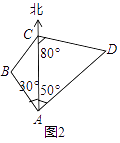
某客轮在A处看港口D在客轮的北偏东50°,A处看灯塔B在客轮的北偏西30°,距离为2 海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
22. 已知:如图,抛物线y=ax2+bx+c与x轴交于两个不同的点A(﹣4,0),B(1,0),与y轴正半轴交于点C,tan∠CAB= .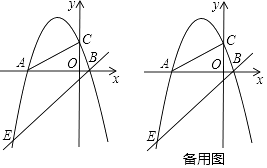 (1)、求抛物线的解析式并验证点Q(﹣1,3)是否在抛物线上;(2)、点M是线段AC上一动点(不与A,C重合),过点M作x轴的垂线,垂足为H,交抛物线于点N,试判断当MN为最大值时,以MN为直径的圆与y轴的位置关系并说明理由;(3)、已知过点B的直线y=x﹣1交抛物线于另一点E,问:在x轴上是否存在点P,使以点P,A,Q为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式并验证点Q(﹣1,3)是否在抛物线上;(2)、点M是线段AC上一动点(不与A,C重合),过点M作x轴的垂线,垂足为H,交抛物线于点N,试判断当MN为最大值时,以MN为直径的圆与y轴的位置关系并说明理由;(3)、已知过点B的直线y=x﹣1交抛物线于另一点E,问:在x轴上是否存在点P,使以点P,A,Q为顶点的三角形与△AEB相似?若存在,请求出所有符合要求的点P的坐标;若不存在,请说明理由.