2016-2017学年湖北省武汉市洪山区七年级下学期期中数学试卷

试卷更新日期：2017-06-26 类型：期中考试

进入出卷网下载

一、选择题

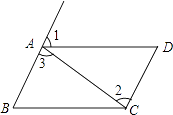
1. 下列各式中，正确的是（）

A、 $\sqrt{16}$ =±4 B、± $\sqrt{16}$ =4 C、 $\sqrt[3]{- 27}$ =﹣3 D、 $\sqrt{{(- 4)}^{2}}$ =﹣4

查看试题解析
2. 如图，能判定AD∥BC的条件是（）

A、∠3=∠2 B、∠1=∠2 C、∠B=∠D D、∠B=∠1

查看试题解析
3. 在平面直角坐标系中，点P（﹣3，2）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 下列说法正确的是（）

A、﹣3是﹣9的平方根 B、3是（﹣3）²的算术平方根 C、（﹣2）²的平方根是2 D、8的立方根是±2

查看试题解析
5. 一个长方形在平面直角坐标系中，若其三个顶点的坐标分别为（﹣3，﹣2），（2，﹣2），（2，1），则第四个顶点为（　　）

A、（2，﹣5） B、（2，2） C、（3，1） D、（﹣3，1）

查看试题解析
6. 如图，一条公路修到湖边时，需拐弯绕道而过，如果第一次拐的角∠A是100°第二次拐的角∠B是150°，第三次拐的角是∠C，这时的道路恰好和第一次拐弯之前的道路平行，则∠C是（）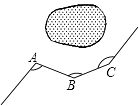

A、120° B、130° C、140° D、150°

查看试题解析
7. 下列各数： $\frac{23}{7}$ 、1.414、0. $\dot{7} \dot{2}$ 、 $\sqrt[3]{- 8}$ 、 $\sqrt[3]{16}$ 中，其中无理数有（）个．

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 如图，AB∥CD，∠P=35°，∠D=100°，则∠ABP的度数是（）

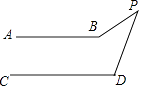A、165° B、145° C、135° D、125°

查看试题解析
9. 比较实数：2、 $\sqrt{5}$ 、 $\sqrt[3]{7}$ 的大小，正确的是（）

A、 $\sqrt[3]{7}$ ＜2＜ $\sqrt{5}$ B、2＜ $\sqrt[3]{7}$ ＜ $\sqrt{5}$ C、 $\sqrt{5}$ ＜ $\sqrt[3]{7}$ ＜2 D、2＜ $\sqrt{5}$ ＜ $\sqrt[3]{7}$

查看试题解析
10. 如图，已知AB∥CD，∠EBF=2∠ABE，∠EDF=2∠CDE，则∠E与∠F之间满足的数量关系是（）

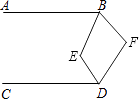A、∠E=∠F B、∠E+∠F=180° C、3∠E+∠F=360° D、2∠E﹣∠F=90°

查看试题解析

二、填空题

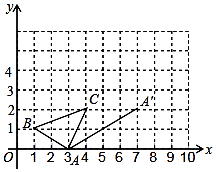
11. 一个正数a的平方根是5x+18与6﹣x，则这个正数a是．

查看试题解析
12. 已知A（1，﹣2）、B（﹣1，2）、E（2，a）、F（b，3），若将线段AB平移至EF，点A、E为对应点，则a+b的值为．

查看试题解析
13.
如图，在直角坐标系中，△ABC的三个顶点均在格点上，其位置如图所示．现将△ABC沿AA′的方向平移，使得点A移至图中的点A′的位置，写出平移过程中线段AB扫过的面积．

查看试题解析
14. 把一张长方形纸片按图中那样折叠后，若得到∠BGD′=40°，则∠C′FE=°．

查看试题解析
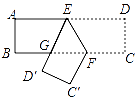15. 如图，长方形BCDE的各边分别平行于x轴或y轴，物体甲和物体乙分别由点A（2，0）同时出发，沿长方形BCDE的边作环绕运动．物体甲按逆时针方向以1个单位/秒匀速运动，物体乙按顺时针方向以2个单位/秒匀速运动，则两个物体运动后的第2017次相遇地点的坐标是．

查看试题解析
16. 如图，已知EF∥GH，A、D为GH上的两点，M、B为EF上的两点，延长AM于点C，AB平分∠DAC，直线DB平分∠FBC，若∠ACB=100°，则∠DBA的度数为．

查看试题解析

三、解答题

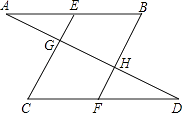
17. 求值或计算：

(1)、求满足条件的x值： $\frac{1}{2}$ x²﹣8=0

(2)、计算： $\sqrt{{(- 3)}^{2}}$ ﹣ $\sqrt[3]{- 64}$ ﹣ $\sqrt{36}$ ．

查看试题解析
18. 如图，已知∠AGE+∠AHF=180°，∠BEC=∠BFC，则∠A与∠D相等吗？下面是童威同学的推导过程，请你帮助他在括号内填上推导依据
∵∠AGE+∠AHF=180°（已知）
∠AGE=∠CGD （）
∴∠CGD+∠AHF=180°
∴CE∥BF （）
∴∠BEC+∠B=180°
∵∠BFC+∠BFD=180°
∠BEC=∠BFC（已知）
∴∠B=∠BFD （）
∴AB∥CD
∴∠A=∠D．

查看试题解析
19. 已知：如图，AE⊥BC，FG⊥BC，∠1=∠2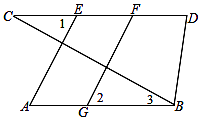

(1)、求证：AB∥CD

(2)、若∠D=∠3+50°，∠CBD=80°，求∠C的度数．

查看试题解析
20. 某区进行课堂教学改革，将学生分成5个学习小组，采取团团坐的方式．如图，这是某校七（1）班教室简图，点A、B、C、D、E分别代表五个学习小组的位置，已知C点的坐标为（﹣2，﹣2）

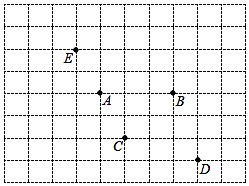(1)、请按题意建立平面直角坐标系（横轴和纵轴均为小正方形的边所在直线，每个小正方形边长为1个单位长度），写出图中其他几个学习小组的坐标；

(2)、过点D作直线DF∥AC交y轴于点F，直接写出点F的坐标．

查看试题解析
21.
△ABC在平面直角坐标系中的位置如图所示，三个顶点A、B、C的坐标分别是（﹣1，4）、（﹣4，﹣1）、（1，1）．将△ABC向右平移5个单位长度，再向上平移1个单位长度，得到△A′BC

(1)、请画出平移后的，并写出的坐标

(2)、若在第四象限内有一点M（4，m），是否存在点M，使得四边形A′OMB′的面积等于△ABC的面积的一半？若存在，请求出点M的坐标；若不存在，请说明理由．

查看试题解析
22. 如图，四边形ABCD中，AD∥BC，∠ADC=α，P为直线CD上一动点，点M在线段BC上，连MP，∠MPD=β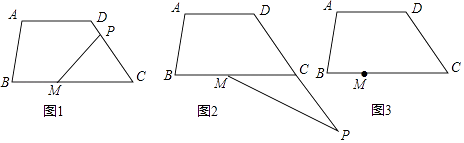

(1)、如图，若MP⊥CD，α=120°，则∠BMP=；

(2)、如图，当P点在DC延长线上时，∠BMP=；

(3)、如图，当P点在CD延长线上时，请画出图形，写出∠BMP、β、α之间的数量关系，并证明你的结论．

查看试题解析
23.
如图，在平面直角坐标系中，点A、B、C、E、P均在坐标轴上，A（0，3）、B（﹣4，0）、P（0，﹣3），点C是线段OP（不包含O、P）上一动点，AB∥CE，延长CE到D，使CD=BA

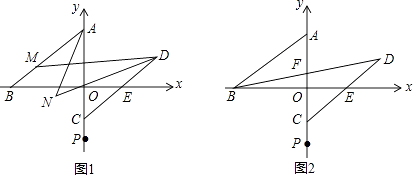(1)、如图，点M在线段AB上，连MD，∠MAO与∠MDC的平分线交于N．若∠BAO=α，∠BMD=130°，则∠AND的度数为

(2)、如图，连BD交y轴于F．若OC=2OF，求点C的坐标

(3)、如图，连BD交y轴于F，在点C运动的过程中， $\frac{A O - O C}{O F}$ 的值是否变化？若不变，求出其值；若变化，请说明理由．

查看试题解析