2017年山东省济南市历下区中考数学二模试卷

试卷更新日期：2017-06-26 类型：中考模拟

进入出卷网下载

一、选择题

1. 下列四个图形中，既是轴对称图形又是中心对称图形的是（　　）

A、 B、 C、 D、

查看试题解析
2. 下列计算正确的是（）

A、2 $\sqrt{\frac{1}{2}}$ = $\sqrt{2}$ B、 $\sqrt{2} + \sqrt{3}$ = $\sqrt{5}$ C、4 $\sqrt{3}$ ﹣3 $\sqrt{3}$ =1 D、3+2 $\sqrt{2}$ =5 $\sqrt{2}$

查看试题解析
3. 我国平均每平方千米的土地一年从太阳得到的能量，相当于燃烧130 000 000kg的煤所产生的能量．把130 000 000kg用科学记数法可表示为（）

A、13×10⁷kg B、0.13×10⁸kg C、1.3×10⁷kg D、1.3×10⁸kg

查看试题解析
4. 如图，AB∥CD，CB平分∠ABD．若∠C=40°，则∠D的度数为（）

A、90° B、100° C、110° D、120°

查看试题解析
5. 平面直角坐标系中，点P（﹣2，3）关于x轴对称的点的坐标为（）

A、（﹣2，﹣3） B、（2，﹣3） C、（﹣3，﹣2） D、（3，﹣2）

查看试题解析
6. 某几何体的主视图、左视图和俯视图分别如图所示，则该几何体的体积为（）

A、3π B、2π C、π D、12

查看试题解析
7. 实施新课改以来，某班学生经常采用“小组合作学习”的方式进行学习，学习委员小兵每周对各小组合作学习的情况进行了综合评分．下表是其中一周的统计数据：
组别
1
2
3
4
5
6
7
分值
90
95
90
88
90
92
85
这组数据的中位数和众数分别是（）

A、88，90 B、90，90 C、88，95 D、90，95

查看试题解析
8. 如图，菱形ABCD中，∠B=60°，AB=4，则以AC为边长的正方形ACEF的周长为（）

A、14 B、15 C、16 D、17

查看试题解析
9. 小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：x﹣y，a﹣b，2，x²﹣y² ， a，x+y，分别对应下列六个字：南、爱、我、美、游、济，现将2a（x²﹣y²）﹣2b（x²﹣y²）因式分解，结果呈现的密码信息可能是（）

A、我爱美 B、济南游 C、我爱济南 D、美我济南

查看试题解析
10. 如图，将正方形OABC放在平面直角坐标系中，O是原点，A的坐标为（1， $\sqrt{3}$ ），则点B的坐标为（）

A、（1﹣ $\sqrt{3}$ ， $\sqrt{3}$ +1） B、（﹣ $\sqrt{3}$ ， $\sqrt{3}$ +1） C、（﹣1， $\sqrt{3}$ +1） D、（﹣1， $\sqrt{3}$ ）

查看试题解析
11. 如图，在Rt△ABC中，∠B=90°，∠A=30°，以点A为圆心，BC长为半径画弧交AB于点D，分别以点A、D为圆心，AB长为半径画弧，两弧交于点E，连接AE，DE，则∠EAD的余弦值是（）

A、 $\frac{\sqrt{3}}{12}$ B、 $\frac{\sqrt{3}}{6}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
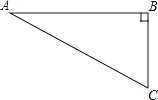12. 如图，反比例函数y= $\frac{k}{x}$ 的图象经过二次函数y=ax²+bx图象的顶点（﹣ $\frac{1}{2}$ ，m）（m＞0），则有（）

A、a=b+2k B、a=b﹣2k C、k＜b＜0 D、a＜k＜0

查看试题解析
13. 一组正方形按如图所示的方式放置，其中顶点B₁在y轴上，顶点C₁、E₁、E₂、C₂、E₃、E₄、C₃…在x轴上，已知正方形A₁B₁C₁D₁的边长为1，∠B₁C₁O=60°，B₁C₁∥B₂C₂∥B₃C₃…，则正方形A₂₀₁₇B₂₀₁₇C₂₀₁₇D₂₀₁₇的边长是（）

A、（ $\frac{1}{2}$ ）²⁰¹⁶ B、（ $\frac{1}{2}$ ）²⁰¹⁷ C、（ $\frac{\sqrt{3}}{3}$ ）²⁰¹⁶ D、（ $\frac{\sqrt{3}}{3}$ ）²⁰¹⁷

查看试题解析
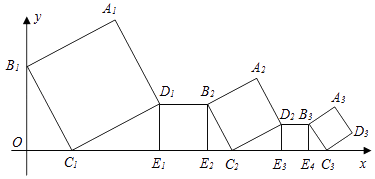14. 定义[a，b，c]为函数y=ax²+bx+c的特征数，下面给出特征数为[2m，1﹣m，﹣1﹣m]的函数的一些结论，其中不正确的是（）

A、当m=﹣3时，函数图象的顶点坐标是（ $\frac{1}{3} ， \frac{8}{3}$ ） B、当m＞0时，函数图象截x轴所得的线段长度大于 $\frac{3}{2}$ C、当m≠0时，函数图象经过同一个点 D、当m＜0时，函数在x $> \frac{1}{4}$ 时，y随x的增大而减小

查看试题解析

二、填空题

15. 比较大小： $2 \sqrt{5}$ $3 \sqrt{2}$ ．

查看试题解析
16. 若关于x的一元二次方程x²+4x+k=0有两个不相等的实数根，则k的取值范围是．

查看试题解析
17. 如图，等腰△ABC中，AB=AC，∠BAC=50°，AB的垂直平分线MN交AC于点D，则∠DBC的度数是．

查看试题解析
18. 如图，量角器的直径与直角三角板ABC的斜边AB重合，其中量角器0刻度线的端点N与点A重合，射线CP从CA处出发沿顺时针方向以每秒3度的速度旋转，CP与量角器的半圆弧交于点E，第24秒，点E在量角器上对应的读数是度.

查看试题解析
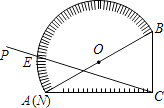19.
如图，M为双曲线y= $\frac{\sqrt{3}}{x}$ 上的一点，过点M作x轴、y轴的垂线，分别交直线y=﹣x+m于点D、C两点，若直线y=﹣x+m与y轴交于点A，与x轴相交于点B，则AD•BC的值为．

查看试题解析
20.
如图，边长为4的正方形ABCD中，P是BC边上一动点（不含B、C点）．将△ABP沿直线AP翻折，点B落在点E处；在CD上有一点M，使得将△CMP沿直线MP翻折后，点C落在直线PE上的点F处，直线PE交CD于点N，连接MA，NA．则以下结论中正确的有（写出所有正确结论的序号）．
①∠NAP=45°；
②当P为BC中点时，AE为线段NP的中垂线；
③四边形AMCB的面积最大值为10；
④线段AM的最小值为2 $\sqrt{5}$ ；
⑤当△ABP≌△ADN时，BP=4 $\sqrt{2}$ ﹣4．

查看试题解析

三、解答题

21. 计算下列各题

(1)、计算：（a﹣b）²﹣a（a﹣2b）；

(2)、解方程： $\frac{2}{x - 3}$ = $\frac{3}{x}$ ．

查看试题解析
22. 解答题

(1)、如图1，AD、BC相交于点O，OA=OC，∠OBD=∠ODB．求证：AB=CD．

(2)、如图2，AB是⊙O的直径，OA=1，AC是⊙O的弦，过点C的切线交AB的延长线于点D，若OD= $\sqrt{2}$ ，求∠BAC的度数．

查看试题解析
23. 某服装店用6000元购进A，B两种新式服装，按标价售出后可获得毛利润3800元（毛利润=售价﹣进价），这两种服装的进价、标价如表所示：
价格类型
A型
B型
进价（元/件）
60
100
标价（元/件）
100
160
求这两种服装各购进的件数．

查看试题解析
24. “宜居襄阳”是我们的共同愿景，空气质量备受人们关注．我市某空气质量监测站点检测了该区域每天的空气质量情况，统计了2013年1月份至4月份若干天的空气质量情况，并绘制了如下两幅不完整的统计图．
请根据图中信息，解答下列问题：

(1)、统计图共统计了天的空气质量情况；

(2)、请将条形统计图补充完整；；
空气质量为“优”所在扇形的圆心角度数是；

(3)、从小源所在环保兴趣小组4名同学（2名男同学，2名女同学）中，随机选取两名同学去该空气质量监测站点参观，则恰好选到一名男同学和一名女同学的概率是

查看试题解析
25.
如图，在平面直角坐标系xOy中，直线y= $\frac{\sqrt{3}}{3}$ x与反比例函数y= $\frac{k}{x}$ 在第一象限内的图象相交于点A（m，3）．

(1)、求该反比例函数的关系式；

(2)、
将直线y= $\frac{\sqrt{3}}{3}$ x沿y轴向上平移8个单位后与反比例函数在第一象限内的图象相交于点B，连接AB，这时恰好AB⊥OA，求tan∠AOB的值；

(3)、在（2）的条件下，在射线OA上存在一点P，使△PAB∽△BAO，求点P的坐标．

查看试题解析
26.
如图1．在菱形ABCD中，AB=2 $\sqrt{5}$ ，tan∠ABC=2，∠BCD=α，点E从点D出发，以每秒1个单位长度的速度沿着射线DA的方向匀速运动，设运动时间为t（秒），将线段CE绕点C顺时针旋转α度，得到对应线段CF，连接BD、EF，BD交EC、EF于点P、Q．

(1)、求证：△ECF∽△BCD；

(2)、当t为何值时，△ECF≌△BCD？

(3)、当t为何值时，△EPQ是直角三角形？

查看试题解析
27.
如图，已知抛物线y=﹣ $\frac{1}{4}$ x²+bx+c交x轴于点A（2，0）、B（一8，0），交y轴于点C，过点A、B、C三点的⊙M与y轴的另一个交点为D．

(1)、求此抛物线的表达式及圆心M的坐标；

(2)、设P为弧BC上任意一点（不与点B，C重合），连接AP交y轴于点N，请问：AP•AN是否为定值，若是，请求出这个值；若不是，请说明理由；

(3)、延长线段BD交抛物线于点E，设点F是线段BE上的任意一点（不含端点），连接AF．动点Q从点A出发，沿线段AF以每秒1个单位的速度运动到点F，再沿线段FB以每秒 $\sqrt{5}$ 个单位的速度运动到点B后停止，问当点F的坐标是多少时，点Q在整个运动过裎中所用时间最少？

查看试题解析

价格类型	A型	B型
进价（元/件）	60	100
标价（元/件）	100	160

组别	1	2	3	4	5	6	7
分值	90	95	90	88	90	92	85