2017年山东省菏泽市东明县中考数学二模试卷

试卷更新日期：2017-06-26 类型：中考模拟

进入出卷网下载

一、选择题。

1. 在实数0，（﹣ $\sqrt{3}$ ）⁰ ，（﹣ $\frac{2}{3}$ ）^﹣² ， |﹣2|中，最大的是（）

A、0 B、（﹣ $\sqrt{3}$ ）⁰ C、（﹣ $\frac{2}{3}$ ）^﹣² D、|﹣2|

查看试题解析
2. 花粉的质量很小，一粒某种植物花粉的质量约为0.000037毫克，已知1克=1000毫克，那么0.000000037毫克可用科学记数法表示为（）

A、3.7×10^﹣⁵克 B、3.7×10^﹣⁶克 C、37×10^﹣⁷克 D、3.7×10^﹣⁸克

查看试题解析
3. 下列银行标志中，既不是中心对称图形也不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列运算正确的是（）

A、x³•x⁵=x¹⁵ B、（x²）⁵=x⁷ C、 $\sqrt[3]{27}$ =3 D、 $\frac{- a + b}{a + b}$ =﹣1

查看试题解析
5. 如果不等式组 $\{\begin{matrix} x > a \\ x < 2 \end{matrix}$ 恰有3个整数解，则a的取值范围是（　　）

A、a≤﹣1 B、a＜﹣1 C、﹣2≤a＜﹣1 D、﹣2＜a≤﹣1

查看试题解析
6. 已知一次函数y₁=kx+b（k＜0）与反比例函数y₂= $\frac{m}{x}$ （m≠0）的图象相交于A、B两点，其横坐标分别是﹣1和3，当y₁＞y₂ ，实数x的取值范围是（）

A、x＜﹣1或0＜x＜3 B、﹣1＜x＜0或0＜x＜3 C、﹣1＜x＜0或x＞3 D、0＜x＜3

查看试题解析
7. 如图，四边形ABCD为平行四边形，延长AD到E，使DE=AD，连接EB，EC，DB，添加一个条件，不能使四边形DBCE成为矩形的是（）

A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE

查看试题解析
8. 如图：二次函数y=ax2+bx+c的图象所示，下列结论中：①abc＞0；②2a+b=0；③当m≠1时，a+b＞am²+bm；④a﹣b+c＞0；⑤若ax₁²+bx₁=ax₂²+bx₂ ，且x₁≠x₂ ，则x₁+x₂=2，正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题。

9. 为了解当地气温变化情况，某研究小组记录了寒假期间连续6天的最高气温，结果如下（单位：℃）：﹣6，﹣3，x，2，﹣1，3，若这组数据的中位数是﹣1，在下列结论中：①方差是8；②极差是9；③众数是﹣1；④平均数是﹣1，其中正确的序号是．

查看试题解析
10. 如图：△ABC中，AB=AC，内切圆⊙O与边BC、AB分别切于点D、E、F，若∠C=30°，CE=2 $\sqrt{3}$ ，则AC= ．

查看试题解析
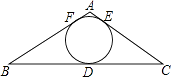11. 因式分解：xy²﹣4x= ．

查看试题解析
12. 已知 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ 是二元一次方程组 ${\begin{matrix} m x + n y = 7 \\ n x - m y = 1 \end{matrix}$ 的解，则m+3n的立方根为．

查看试题解析
13. 化简 $\frac{m - 1}{m}$ ÷ $\frac{1 - m}{m^{2}}$ 是．

查看试题解析
14. 如图，点A在双曲线y= $\frac{3}{x}$ 上，点B在双曲线y= $\frac{k}{x}$ （k≠0）上，AB∥x轴，过点A作AD⊥x轴于D，连接OB，与AD相交于点C，若AC=2CD，则k的值为．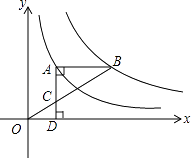

查看试题解析

三、解答题。

15. 先化简，再求值：（x+1）²+x（2﹣x），其中x= $\sqrt{2}$ ．

查看试题解析
16. 解不等式组： ${\begin{matrix} 2 x + 5 \leq 3 (x + 2) \\ 2 x - \frac{1 + 3 x}{2} < 1 \end{matrix}$ ，并写出它的非负整数解．

查看试题解析
17. 如图，将矩形纸片ABCD沿对角线BD折叠，使点A落在平面上的F点处，DF交BC于点E．

(1)、求证：△DCE≌△BFE；

(2)、若CD=2，∠ADB=30°，求BE的长．

查看试题解析
18.
2016年3月，我市某中学举行了“爱我中国•朗诵比赛”活动，根据学生的成绩划分为A、B、C、D四个等级，并绘制了不完整的两种统计图．根据图中提供的信息，回答下列问题：

(1)、参加朗诵比赛的学生共有人，并把条形统计图补充完整；

(2)、扇形统计图中，m= ， n=；C等级对应扇形有圆心角为度；

(3)、学校欲从获A等级的学生中随机选取2人，参加市举办的朗诵比赛，请利用列表法或树形图法，求获A等级的小明参加市朗诵比赛的概率．

查看试题解析
19. 今年我市某公司分两次采购了一批大蒜，第一次花费40万元，第二次花费60万元．已知第一次采购时每吨大蒜的价格比去年的平均价格上涨了500元，第二次采购时每吨大蒜的价格比去年的平均价格下降了500元，第二次的采购数量是第一次采购数量的两倍．

(1)、试问去年每吨大蒜的平均价格是多少元？

(2)、该公司可将大蒜加工成蒜粉或蒜片，若单独加工成蒜粉，每天可加工8吨大蒜，每吨大蒜获利1000元；若单独加工成蒜片，每天可加工12吨大蒜，每吨大蒜获利600元．由于出口需要，所有采购的大蒜必需在30天内加工完毕，且加工蒜粉的大蒜数量不少于加工蒜片的大蒜数量的一半，为获得最大利润，应将多少吨大蒜加工成蒜粉？最大利润为多少？

查看试题解析
20.
如图1，已知双曲线y= $\frac{k}{x}$ （k＞0）与直线y=k′x交于A、B两点，点A在第一象限，试回答下列问题：

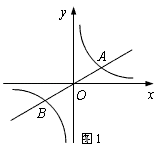(1)、若点A的坐标为（3，1），则点B的坐标为；当x满足：时， $\frac{k}{x}$ ≤k′x；

(2)、
如图2，过原点O作另一条直线l，交双曲线y= $\frac{k}{x}$ （k＞0）于P，Q两点，点P在第一象限．
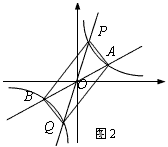
四边形APBQ一定是；

(3)、若点A的坐标为（3，1），点P的横坐标为1，求四边形APBQ的面积．

(4)、设点A，P的横坐标分别为m，n，四边形APBQ可能是矩形吗？可能是正方形吗？若可能，直接写出m，n应满足的条件；若不可能，请说明理由．

查看试题解析
21.
已知：△ABC是边长为4的等边三角形，点O在边AB上，⊙O过点B且分别与边AB，BC相交于点D，E，EF⊥AC，垂足为F．

(1)、求证：直线EF是⊙O的切线；

(2)、当直线DF与⊙O相切时，求⊙O的半径．

查看试题解析
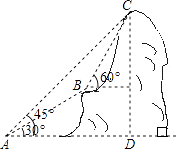
22.
如图，某电信部门计划修建一条连接B、C两地的电缆．测量人员在山脚A点测得B、C两地的仰角分别为30°、45°，在B地测得C地的仰角为60°．已知C地比A地高200m，电缆BC至少长多少米（精确到1m）？

查看试题解析
23.
如图，△ABC和△ADE是有公共顶点的等腰直角三角形，∠BAC=∠DAE=90°，点P为射线BD，CE的交点．

(1)、求证：BD=CE；

(2)、若AB=2，AD=1，把△ADE绕点A旋转，
①当∠EAC=90°时，求PB的长；
②直接写出旋转过程中线段PB长的最小值与最大值．

查看试题解析
24. 如图：抛物线y=ax²+bx+c交y轴于点C（0，4），对称轴x=2与x轴交于点D，顶点为M，且DM=OC+OD，

(1)、求抛物线的解析式；

(2)、设点P（x，y）是第一象限内该抛物线上的一个动点，△PCD的面积为S，求S关于x的函数关系式，写出自变量x的取值范围，并求当x取多少时，S的值最大，最大是多少？

查看试题解析