2017年山东省菏泽市曹县中考数学二模试卷
试卷更新日期:2017-06-26 类型:中考模拟
一、选择题。
-
1. 3﹣2的相反数是( )A、9 B、﹣9 C、 D、﹣2. 若点A(a+1,b﹣1)在第二象限,则点B(﹣a,b+2)在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列几何体是由4个相同的小正方体搭成的,其中主视图和左视图相同的是( )
A、 B、
B、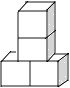 C、
C、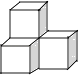 D、
D、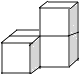 4. 某学习小组10名学生参加数学竞赛,他们的得分情况如下表:
4. 某学习小组10名学生参加数学竞赛,他们的得分情况如下表:人数(人)
2
3
4
1
分数(分)
80
85
90
95
那么这10名学生所得分数的众数和中位数分别是( )
A、90,90 B、90,85 C、90,87.5 D、85,855. 将矩形纸片ABCD按如图所示的方式折叠,AE,EF为折痕,∠BAE=30°,AB= ,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为( )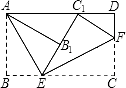 A、 B、2 C、3 D、26. 如图,点A是反比例函数y= 的图象上的一点,过A作▱ABCD,使点B在x轴上,点D在y轴上,已知▱ABCD的面积为6,则k的值为( )
A、 B、2 C、3 D、26. 如图,点A是反比例函数y= 的图象上的一点,过A作▱ABCD,使点B在x轴上,点D在y轴上,已知▱ABCD的面积为6,则k的值为( )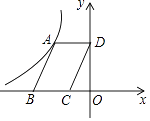 A、3 B、﹣3 C、6 D、﹣67. 如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )
A、3 B、﹣3 C、6 D、﹣67. 如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于( )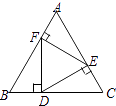 A、1:3 B、2:3 C、 :2 D、 :38. 如图,直线y= x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A、1:3 B、2:3 C、 :2 D、 :38. 如图,直线y= x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )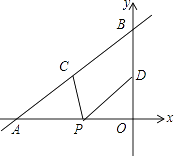 A、(﹣3,0) B、(﹣6,0) C、(﹣ ,0) D、(﹣ ,0)
A、(﹣3,0) B、(﹣6,0) C、(﹣ ,0) D、(﹣ ,0)二、填空题
-
9. 分解因式4(a﹣b)+a2(b﹣a)的结果是 .10. 将一个圆心角为120°,半径为6cm的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为 .11. 已知方程组 ,则x+y的值为 .12. 如图,半径为3的⊙A经过原点O和点C(0,2),B是⊙O上一点,则tan∠OBC为 .
 13. 如图,在△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= .
13. 如图,在△ABC中,∠C=90°,AC=BC= ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= . 14. 在Rt△ABC中,∠ABC=90°,AB=4,BC=2.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,点C到原点的最大距离为 .
14. 在Rt△ABC中,∠ABC=90°,AB=4,BC=2.如图,将直角顶点B放在原点,点A放在y轴正半轴上,当点B在x轴上向右移动时,点A也随之在y轴上向下移动,当点A到达原点时,点B停止移动,在移动过程中,点C到原点的最大距离为 .
三、解答题
-
15. 解方程:x2+4x﹣2=016. 解不等式 .17. 已知x﹣2y=﹣3,求(x+2)2﹣6x+4y(y﹣x+1)的值.18. 如图,四边形ABCD中,CD=3,BD=2 ,sin∠DBC= ,求BC的长.
 19. 某电子元件厂准备生产1200个电子元件,生产一半后,由于要尽快投入市场,该厂提高了生产效率,每天生产的电子元件个数是原来的1.2倍,结果提前2天完成了任务,求该厂后来每天生产电子元件多少个?20. 如图,OA⊥OB,AB⊥x轴于C,点A( ,1)在反比例函数y= 的图象上.
19. 某电子元件厂准备生产1200个电子元件,生产一半后,由于要尽快投入市场,该厂提高了生产效率,每天生产的电子元件个数是原来的1.2倍,结果提前2天完成了任务,求该厂后来每天生产电子元件多少个?20. 如图,OA⊥OB,AB⊥x轴于C,点A( ,1)在反比例函数y= 的图象上. (1)、求反比例函数y= 的表达式;(2)、在x轴的负半轴上存在一点P,使S△AOP= S△AOB , 求点P的坐标.21. 甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.(1)、求三次传球后,球回到甲脚下的概率;(2)、三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?22. 如图,AB是⊙O的直径,C为⊙O上一点,PC切⊙O于C,AE⊥PC交PC的延长线于E,AE交⊙O于D,PC与AB的延长线相交于点P,连接AC、BC.
(1)、求反比例函数y= 的表达式;(2)、在x轴的负半轴上存在一点P,使S△AOP= S△AOB , 求点P的坐标.21. 甲、乙、丙三位同学进行足球传球训练,球从一个人脚下随机传到另一个人脚下,且每位传球人传给其余两人的机会是均等的,由甲开始传球,共传三次.(1)、求三次传球后,球回到甲脚下的概率;(2)、三次传球后,球回到甲脚下的概率大还是传到乙脚下的概率大?22. 如图,AB是⊙O的直径,C为⊙O上一点,PC切⊙O于C,AE⊥PC交PC的延长线于E,AE交⊙O于D,PC与AB的延长线相交于点P,连接AC、BC. (1)、求证:AC平分∠BAD;(2)、若PB:PC=1:2,PB=4,求AB的长.23. 如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)
(1)、求证:AC平分∠BAD;(2)、若PB:PC=1:2,PB=4,求AB的长.23. 如图,四边形ABCD中,AD∥BC,∠A=90°,AD=1cm,AB=3cm,BC=5cm,动点P从点B出发以1cm/s的速度沿BC的方向运动,动点Q从点C出发以2cm/s的速度沿CD方向运动,P、Q两点同时出发,当Q到达点D时停止运动,点P也随之停止,设运动的时间为ts(t>0)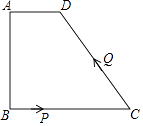 (1)、求线段CD的长;(2)、t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?24. 如图,抛物线y=﹣x2﹣2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点.
(1)、求线段CD的长;(2)、t为何值时,线段PQ将四边形ABCD的面积分为1:2两部分?24. 如图,抛物线y=﹣x2﹣2x+3的图象与x轴交A、B两点,与y轴交于点C,点D为抛物线的顶点. (1)、求点A、B、C的坐标;(2)、点M为线段AB上一点(点M不与点A、B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积;(3)、在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=2 DQ,求点F的坐标.
(1)、求点A、B、C的坐标;(2)、点M为线段AB上一点(点M不与点A、B重合),过M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过P作PQ∥AB交抛物线于点Q,过Q作QN⊥x轴于N,当矩形PMNQ的周长最大时,求△AEM的面积;(3)、在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ,过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方),若FG=2 DQ,求点F的坐标.