2017年江西省鹰潭市中考数学模拟试卷
试卷更新日期:2017-06-26 类型:中考模拟
一、选择题
-
1. 李刚同学拿一个矩形木框在阳光下摆弄,矩形木框在地面上形成的投影不可能是( )A、
 B、
B、 C、
C、 D、
D、 2. 如果不等式组恰有3个整数解,则a的取值范围是( )A、a≤﹣1 B、a<﹣1 C、﹣2≤a<﹣1 D、﹣2<a≤﹣13. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( )
2. 如果不等式组恰有3个整数解,则a的取值范围是( )A、a≤﹣1 B、a<﹣1 C、﹣2≤a<﹣1 D、﹣2<a≤﹣13. 如图,是某几何体的三视图及相关数据,则该几何体的侧面积是( ) A、10π B、15π C、20π D、30π4. 互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为( )A、120元 B、100元 C、80元 D、60元5. 如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )
A、10π B、15π C、20π D、30π4. 互联网“微商”经营已成为大众创业新途径,某微信平台上一件商品标价为200元,按标价的五折销售,仍可获利20元,则这件商品的进价为( )A、120元 B、100元 C、80元 D、60元5. 如图所示,向一个半径为R、容积为V的球形容器内注水,则能够反映容器内水的体积y与容器内水深x间的函数关系的图象可能是( )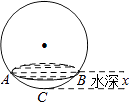 A、
A、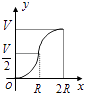 B、
B、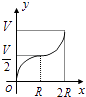 C、
C、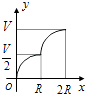 D、
D、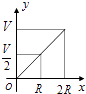 6. 如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( )
6. 如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题:
-
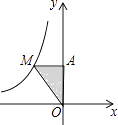
7. 分解因式:a3﹣2a2+a= .8. 若 tan(x+10°)=1,则锐角x的度数为 .9. 如图:M为反比例函数 图象上一点,MA⊥y轴于A,S△MAO=2时,k= .
 10. 关于x的分式方程 的解为正数,则m的取值范围是 .11. 在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF= .
10. 关于x的分式方程 的解为正数,则m的取值范围是 .11. 在平行四边形ABCD中,E是CD上一点,DE:EC=1:3,连AE,BE,BD且AE,BD交于F,则S△DEF:S△EBF:S△ABF= .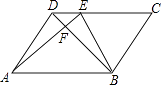 12. 两个反比例函数y= (k>1)和y= 在第一象限内的图象如图所示,点P在y= 的图象上,PC⊥x轴于点C,交y= 的图象于点A,PD⊥y轴于点D,交y= 的图象于点B,BE⊥x轴于点E,当点P在y= 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是(填序号)
12. 两个反比例函数y= (k>1)和y= 在第一象限内的图象如图所示,点P在y= 的图象上,PC⊥x轴于点C,交y= 的图象于点A,PD⊥y轴于点D,交y= 的图象于点B,BE⊥x轴于点E,当点P在y= 图象上运动时,以下结论:①BA与DC始终平行;②PA与PB始终相等;③四边形PAOB的面积不会发生变化;④△OBA的面积等于四边形ACEB的面积.其中一定正确的是(填序号)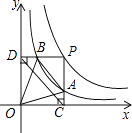
三、解答题:
-
13. 计算下列各题(1)、 ﹣3tan30°+(4﹣π)0﹣( )﹣1(2)、先化简,再求值:( ﹣x+1)÷ ,其中x= ﹣2.14. 在一个木箱中装有卡片共50张,这些卡片共有三种,它们分别标有1、2、3的字样,除此之外其他都相同,其中标有数字2的卡片的张数是标有数字3卡片的张数的3倍少8张.已知从箱子中随机摸出一张标有数字1卡片的概率是 .(1)、求木箱中装有标1的卡片张数;(2)、求从箱子中随机摸出一张标有数字3的卡片的概率.15.
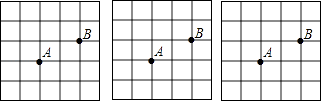
已知下面是3个5×5的正方形网格,小正方形边长都为1,A、B两点在小网格的顶点上,位置如图所示.现请你分别在三个网格中各画一个△ABC.要求:(1)顶点C在网格的顶点上;(2)工具只用无刻度的直尺;(3)所画的3个三角形互不全等,但面积都为2.
 16. 某校食堂的中餐与晚餐的资费标准如下:
16. 某校食堂的中餐与晚餐的资费标准如下:种类
单价
米饭
0.5元/份
A类套餐菜
3.5元/份
B类套餐菜
2.5元/份
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐,这五天共消费36元.请问小杰在这五天内,A,B类套餐菜各选用了多少次?
17.如图是放在水平地面上的一把椅子的侧面图,椅子高为AC,椅面宽为BE,椅脚高为ED,且AC⊥BE,AC⊥CD,AC∥ED.从点A测得点D、E的俯角分别为64°和53°.已知ED=35cm,求椅子高AC约为多少?
(参考数据:tan53°≈ ,sin53°≈ ,tan64°≈2,sin64°≈ )

四、解答题:
-
18.
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
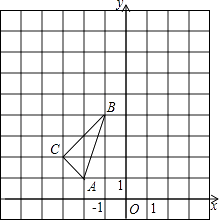 (1)、①画出△ABC关于y轴对称的图形△A1B1C1 , 并直接写出C1点坐标;
(1)、①画出△ABC关于y轴对称的图形△A1B1C1 , 并直接写出C1点坐标;②以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2 , 并直接写出C2点坐标;
(2)、如果点D(a,b)在线段AB上,请直接写出经过(1)②的变化后点D的对应点D2的坐标.
19. 已知:如图1,△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F. (1)、求证:直线EF是⊙O的切线;(2)、如图2,当直线AC与⊙O相切时,求⊙O的半径.
(1)、求证:直线EF是⊙O的切线;(2)、如图2,当直线AC与⊙O相切时,求⊙O的半径.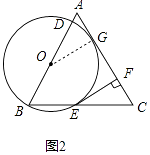 20. 某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.
20. 某地区在一次九年级数学做了检测中,有一道满分8分的解答题,按评分标准,所有考生的得分只有四种:0分,3分,5分,8分.老师为了了解学生的得分情况与题目的难易情况,从全区4500名考生的试卷中随机抽取一部分,通过分析与整理,绘制了如下两幅图不完整的统计图.请根据以上信息解答下列问题:
(1)、填空:a= , b= , 并把条形统计图补全;(2)、请估计该地区此题得满分(即8分)的学生人数;(3)、已知难度系数的计算公式为L= ,其中L为难度系数,X为样本平均得分,W为试题满分值.一般来说,根据试题的难度系数可将试题分为以下三类:当0<L≤0.4时,此题为难题;当0.4<L≤0.7时,此题为中等难度试题;当0.7<L<1时,此题为容易题.试问此题对于该地区的九年级学生来说属于哪一类?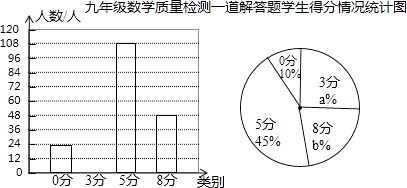
五、解答题:
-
21. 如图,在平面直角坐标系xOy中,一次函数y=kx+b(k≠0)的图象与反比例函数 的图象交于二四象限内的A、B 两点,与x轴交于C点,点B的坐标为(6,n),线段OA=5,E为x轴负半轴上一点,且sin∠AOE= .
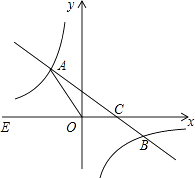 (1)、求该反比例函数和一次函数的解析式;(2)、求△AOC的面积;(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.22.
(1)、求该反比例函数和一次函数的解析式;(2)、求△AOC的面积;(3)、直接写出一次函数值大于反比例函数值时自变量x的取值范围.22.如图,已知四边形ABCD为正方形,AB=2 ,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
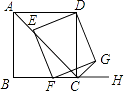 (1)、求证:矩形DEFG是正方形;(2)、探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;(3)、设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.
(1)、求证:矩形DEFG是正方形;(2)、探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由;(3)、设AE=x,四边形DEFG的面积为S,求出S与x的函数关系式.六、解答题:
-
23.
如图1,抛物线C:y=x2经过变化可得到抛物线C1:y1=a1x(x﹣b1),C1与x轴的正半轴交与点A1 , 且其对称轴分别交抛物线C,C1于点B1 , D1 , 此时四边形OB1A1D1恰为正方形;按上述类似方法,如图2,抛物线C1:y1=a1x(x﹣b1)经过变换可得到抛物线C2:y2=a2x(x﹣b2),C2与x轴的正半轴交与点A2 , 且其对称轴分别交抛物线C1 , C2于点B2 , D2 , 此时四边形OB2A2D2也恰为正方形;按上述类似方法,如图3,可得到抛物线C3:y3=a3x(x﹣b3)与正方形OB3A3D3 . 请探究以下问题:
 (1)、填空:a1= , b1=;(2)、求出C2与C3的解析式;(3)、按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).
(1)、填空:a1= , b1=;(2)、求出C2与C3的解析式;(3)、按上述类似方法,可得到抛物线Cn:yn=anx(x﹣bn)与正方形OBnAnDn(n≥1).①请用含n的代数式直接表示出Cn的解析式;
②当x取任意不为0的实数时,试比较y2015与y2016的函数值的大小并说明理由.