2017年江苏省扬州市江都区中考数学一模试卷

试卷更新日期：2017-06-26 类型：中考模拟

进入出卷网下载

一、选择题

1. 比﹣2小1的数是（）

A、﹣1 B、﹣3 C、1 D、3

查看试题解析
2. 函数y= $\sqrt{x + 1}$ 中自变量x的取值范围是（）

A、x＞﹣1 B、x≥﹣1 C、x＜﹣1 D、x≤﹣1

查看试题解析
3. 下列运算正确的是（）

A、 $\sqrt{6}$ ﹣ $\sqrt{3}$ = $\sqrt{3}$ B、 $\sqrt{{(- 3)}^{2}}$ =﹣3 C、a•a²=a² D、（2a³）²=4a⁶

查看试题解析
4. 用5个完全相同的小正方体组合成如图所示的立体图形，它的主视图为（）

A、 B、 C、 D、

查看试题解析
5. 如图是一个可以自由转动的正六边形转盘，其中三个正三角形涂有阴影．转动指针，指针落在有阴影的区域内的概率为a；投掷一枚硬币，正面向上的概率为b．关于a，b大小的正确判断是（）

A、a＞b B、a＜b C、a=b D、不能判断

查看试题解析
6. 某学习小组9名学生参加“数学竞赛”，他们的得分情况如表：
人数（人）
1
3
4
1
分数（分）
80
85
90
95
那么这9名学生所得分数的众数和中位数分别是（）

A、90，90 B、90，85 C、90，87.5 D、85，85

查看试题解析
7.
将一块等腰直角三角板与一把直尺如图放置，若∠1=60°，则∠2的度数为（　　）

A、85° B、75° C、60° D、45°

查看试题解析
8. 如图，点A与点B分别在函数y= $\frac{k_{1}}{x} (k_{1} > 0)$ 与y= $\frac{k_{2}}{x} (k_{2} < 0)$ 的图象上，线段AB的中点M在y轴上．若△AOB的面积为2，则k₁﹣k₂的值是（）

A、2 B、3 C、4 D、5

查看试题解析

二、填空题

9. 2016年，扬州泰州机场升级为国际机场，全年旅客吞吐量143.7万人次．将143.7万用科学记数法表示为．

查看试题解析
10. 分解因式：2x²﹣4x+2= ．

查看试题解析
11. 已知x=2是关于x的方程a（x+1）= $\frac{1}{2}$ a+x的解，则a的值是．

查看试题解析
12. 若2m﹣n²=4，则代数式10+4m﹣2n²的值为．

查看试题解析
13. 一个多边形的每个外角都是60°，则这个多边形边数为．

查看试题解析
14. 如图，在⊙O的内接四边形ABCD中，AB=AD，∠C=110°．若点E在 $\hat{A D}$ 上，则∠E=°．

查看试题解析
15. 当x=m和x=n（m≠n）时，二次函数y=x²﹣2x+3的函数值相等，当x=m+n时，函数y=x²﹣2x+3的值为．

查看试题解析
16. 如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交 $\hat{A B}$ 于点E，以点O为圆心，OC的长为半径作 $\hat{C D}$ 交OB于点D．若OA=2，则阴影部分的面积为．

查看试题解析
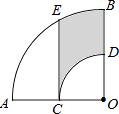17. 如图，在正方形ABCD中，点E为AD的中点，连接EC，过点E作EF⊥EC，交AB于点F，则tan∠ECF= ．

查看试题解析
18. 在Rt△ABC中，∠ACB=90°，AC=8，BC=6，点D是以点A为圆心4为半径的圆上一点，连接BD，点M为BD中点，线段CM长度的最大值为．

查看试题解析

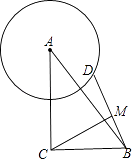
三、解答题

19. 计算下列各题

(1)、计算：（﹣ $\frac{1}{2}$ ）^﹣²﹣|2﹣ $\sqrt{3}$ |﹣3tan30°；

(2)、解不等式组： ${\begin{matrix} 3 x > x + 2 \\ 4 x < 3 (x + 1) \end{matrix}$ ．

查看试题解析
20. 已知x，y满足方程组 ${\begin{matrix} x - 2 y = - 5 \\ 2 x + y = 0 \end{matrix}$ ，求代数式（x﹣y）²﹣（x+2y）（x﹣2y）的值．

查看试题解析
21. 为深化义务教育课程改革，满足学生的个性化学习需求，某校就“学生对知识拓展，体育特长、艺术特长和实践活动四类选课意向”进行了抽样调查（每人选报一类），绘制了如图所示的两幅不完整的统计图，请根据图中信息，解答下列问题：

(1)、求扇形统计图中m的值；

(2)、补全条形统计图；

(3)、已知该校有800名学生，计划开设“实践活动类”课程每班安排20人，问学校开设多少个“实践活动类”课程的班级比较合理？

查看试题解析
22. 在一个不透明的袋子中装有仅颜色不同的5个小球，其中红球3个，黑球2个．

(1)、先从袋中取出m（m＞1）个红球，再从袋子中随机摸出1个球，将“摸出黑球”记为事件A，填空：若A为必然事件，则m的值为，若A为随机事件，则m的取值为；

(2)、若从袋中随机摸出2个球，正好红球、黑球各1个，求这个事件的概率．

查看试题解析
23. 如图，四边形ABCD为平行四边形，E为BC的中点，连接AE并延长交DC的延长线于点F．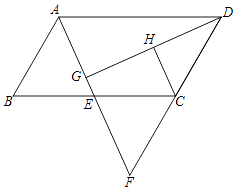

(1)、求证：△ABE≌△FCE；

(2)、过点D作DG⊥AE于点G，H为DG的中点．判断CH与DG的位置关系，
并说明理由．

查看试题解析
24. 目前，步行已成为人们最喜爱的健身方法之一，通过手机可以计算行走的步数与相应的能量消耗．对比手机数据发现：小琼步行13500步与小刚步行9000步消耗的能量相同，若每消耗1千卡能量小琼行走的步数比小刚多15步，求小刚每消耗1千卡能量需要行走多少步？

查看试题解析
25. 如图，AB为⊙O的直径，PB、PC分别是⊙O的切线，切点为B、C，PC、BA的延长线交于点D，DE⊥PO，交PO的延长线于点E．

(1)、求证：∠DPO=∠EDB；

(2)、若PB=3，DB=4，求⊙O的半径．

查看试题解析
26. 随着某市养老机构（养老机构指社会福利院、养老院、社区养老中心等）建设稳步推进，拥有的养老床位不断增加．

(1)、该市的养老床位数从2013年底的2万个增长到2015年底的2.88万个，求该市这两年（从2013年度到2015年底）拥有的养老床位数的平均年增长率；

(2)、若该市某社区今年准备新建一养老中心，其中规划建造三类养老专用房间共100间，这三类养老专用房间分别为单人间（1个养老床位），双人间（2个养老床位），三人间（3个养老床位），因实际需要，单人间房间数在10至30之间（包括10和30），且双人间的房间数是单人间的2倍，设规划建造单人间的房间数为t．
①若该养老中心建成后可提供养老床位200个，求t的值；
②求该养老中心建成后最多提供养老床位多少个？最少提供养老床位多少个？

查看试题解析
27.
如图1，四边形ABCD是正方形，动点P从点A出发，以2cm/s的速度沿边AB、BC、CD匀速运动到D终止；动点Q从A出发，以1cm/s的速度沿边AD匀速运动到D终止，若P、Q两点同时出发，运动时间为ts，△APQ的面积为Scm² ． S与t之间函数关系的图象如图2所示．

(1)、求图2中线段FG所表示的函数关系式；

(2)、当动点P在边AB运动的过程中，若以C、P、Q为顶点的三角形是等腰三角形，求t的值；

(3)、是否存在这样的t，使PQ将正方形ABCD的面积恰好分成1：3的两部分？若存在，求出这样的t的值；若不存在，请说明理由．

查看试题解析
28.
如图，二次函数y=mx²+（m²﹣m）x﹣2m+1的图象与x轴交于点A、B，与y轴交于点C，顶点D的横坐标为1．

(1)、求二次函数的表达式及A、B的坐标；

(2)、若P（0，t）（t＜﹣1）是y轴上一点，Q（﹣5，0），将点Q绕着点P顺时针方向旋转90°得到点E．当点E恰好在该二次函数的图象上时，求t的值；

(3)、在（2）的条件下，连接AD、AE．若M是该二次函数图象上一点，且∠DAE=∠MCB，求点M的坐标．

查看试题解析

人数（人）	1	3	4	1
分数（分）	80	85	90	95