2017年江苏省扬州市高邮市中考数学一模试卷
试卷更新日期：2017-06-26 类型：中考模拟
一、选择题
-
1. 1不是﹣1的（ ）A、 相反数 B、绝对值 C、倒数 D、平方数2. 右图是某几何体的三视图，这个几何体是（ ）
A、圆柱 B、三棱柱 C、球 D、圆锥3. 体育委员把全班45名同学的体育锻炼时间，并绘制了如图所示的折线统计图，则全班45名同学一周的体育锻炼总时间的众数和中位数分别是（ ）
A、9，9 B、9，10 C、18，9 D、18，184. 已知不透明的袋中只装有黑、白两种球，这些球除颜色外都相同，其中白球有2个，黑球有n个，随机地从袋中摸出一个球，记录下颜色后，放回袋子中并摇匀，经过大量重复试验发现摸出白球的频率稳定在0.4附近，则n的值为（ ）A、2 B、3 C、4 D、55. 若锐角α的正弦值为0.58，则（ ）A、α=30° B、α=45° C、30°＜α＜45° D、45°＜α＜30°6. 如图，在平面直角坐标系上，△ABC的顶点A和C分别在x轴、y轴的正半轴上，且AB∥y轴，点B（1，3），将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE，恰好有一反比例函数y= 图象恰好过点D，则k的值为（ ）
A、6 B、﹣6 C、9 D、﹣97. 若数轴上的A、B、C三点表示的实数分别为a、1、﹣1，则|a+1|表示（ ）A、A、B两点间的距离 B、A、C两点间的距离 C、A、B两点到原点的距离之和 D、A、C两点到原点的距离之和8. 已知抛物线y=x2+bx+c的对称轴为x=2，若关于x的一元二次方程﹣x2﹣bx﹣c=0在﹣1＜x＜3的范围内有一个实数根，则c的取值范围是（ ）A、c=4 B、﹣5＜c≤4 C、﹣5＜c＜3或c=4 D、﹣5＜c≤3或c=4二、填空题
-
9. 若a、b、c、d满足 = = ，则 = ．10. 2016年11月10日，记者从民政部召开的会议了解到，目前全国农村留守儿童数量为902万人，“902万”用科学记数法表示为 ．
11. 如图，四边形ABCD是⊙O的内接四边形，∠B=137°，则∠AOC的度数为 ．
12. 如图，若棋盘中“帅”的坐标是（0，1），“卒”的坐标是（2，2），则“马”的坐标是 ．
13. 如图，已知射线OM，以O为圆心，以12cm为半径画弧，与射线OM交于点A，再以点A为圆心，AO长为半径画弧，两弧交于点B，画射线OB，则扇形AOB的面积为 cm2 ．
14. 若点A（﹣1，4）、B（m，4）都在抛物线y=a（x﹣3）2+h上，则m的值为 ．15. 如图，△ABC中，AB=12，AC=8，AD、AE分别是其角平分线和中线，过点C作CG⊥AD于F，交AB于G，连接EF，则线段EF的长为 ．
16. 如图，正方形ABCD的四个顶点A、B、C、D正好分别在四条平行线l1、l3、l4、l2上．若从上到下每两条平行线间的距离都是2cm，则正方形ABCD的面积为 cm2 ．
17. 如图，点M是Rt△ABC的斜边AB的中点，连接CM，作线段CM的垂直平分线，分别交边CB和CA的延长线于点D、E，若∠C=90°，AB=20，tanB= ，则DE= ．
18. 如图，点C在以AB为直径的半圆上，AB=4 ，AC=4，点D在线段AB上运动，点E与点D关于AC对称，DF⊥DE，DF交EC的延长线于点F，当点D从点A运动到点B时，线段EF扫过的面积是 ．
三、解答题
-
19. 计算： ﹣cos45°+（1﹣ ）2 ．20. 因式分解：﹣3a3b+6a2b2﹣3ab3 ．21. 先化简，再求值：（1﹣ ）÷ ，其中x=﹣2．22. 解不等式组 并写出它的所有非负整数解．23. 体育中考前，抽样调查了九年级学生的“1分钟跳绳”成绩，并绘制成了下面的频数分布直方图（每小组含最小值，不含最大值）和扇形图．
(1)、补全频数分布直方图；(2)、扇形图中m=；(3)、若“1分钟跳绳”成绩大于或等于140次为优秀，则估计全市九年级5900名学生中“1分钟跳绳”成绩为优秀的大约有多少人？24. 王老师、张老师、李老师（女），姚老师四位数学老师报名参加了临城片青年教师优秀课选拔赛，将通过抽签决定上课节次，抽签时女士优先(1)、先抽取的李老师不希望上第一节课，却偏偏抽到上第一节课的概率是；(2)、在李老师已经抽到上第一节课的条件下，求抽签结果中，王老师比姚老师先上课的概率．25. 快走是大众常用的健身方式，手机中的“乐动力”可以计算行走的步数与消耗的相应能量，对比数据发现小明步行1200步与小红步行9000步消耗的能量相同，若每消耗1千卡能量小明行走的步数比小红多2步，求小红每消耗1千卡能量可以行走多少步？26. 如图，已知矩形ABCD的两条对角线相交于点O，过点A作AG⊥BD分别交BD、BC于点G、E．
(1)、求证：BE2=EG•EA；(2)、连接CG，若BE=CE，求证：∠ECG=∠EAC．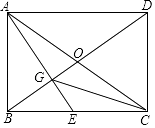
27. 某商场经营某种品牌的玩具，进价是20元，根据市场调查：在一段时间内，销售单价是30元时，销售量是500件，而销售单价每涨1元，就会少售出10件玩具．(1)、不妨设该种品牌玩具的销售单价为x元（x＞40），请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元，并把结果填写在表格中：销售单价（元）
x
销售量y（件）
销售玩具获得利润w（元）
(2)、在（1）问条件下，若商场获得了8000元销售利润，求该玩具销售单价x应定为多少元．(3)、在（1）问条件下，若玩具车规定该品牌玩具销售单价不低于35元，且商场要完成不少于350件的销售任务，求商场销售该品牌服装获得的最大利润是多少？28. 如图，已知直线l与⊙O相离，OA⊥l于点A，交⊙O于点P，点B是⊙O上一点，连接BP并延长，交直线l于点C，使得AB=AC．
(1)、求证：AB是⊙O的切线；(2)、PC=2 ，OA=4．①求⊙O的半径；
②求线段PB的长．
29. 问题：探究一次函数y=kx+k+2（k是不为0常数）图象的共性特点，探究过程：小明尝试把x=﹣1代入时，发现可以消去k，竟然求出了y=2．老师问：结合一次函数图象，这说明了什么？小组讨论得出：无论k取何值，一次函数y=kx+k+2的图象一定经过定点（﹣1，2），老师：如果一次函数的图象是经过某一个定点的直线，那么我们把像这样的一次函数的图象定义为“点旋转直线”．已知一次函数y=（k+3）x+（k﹣1）的图象是“点选直线”(1)、一次函数y=（k+3）x+（k﹣1）的图象经过的顶点P的坐标是 ．(2)、已知一次函数y=（k+3）x+（k﹣1）的图象与x轴、y轴分别相交于点A、B
①若△OBP的面积为3，求k值；
②若△AOB的面积为1，求k值．
