上海市松江区2018-2019学年九年级上学期数学期中考试试卷

试卷更新日期：2019-08-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形一定是相似图形的是（）

A、两个矩形 B、两个周长相等的直角三角形 C、两个正方形 D、两个等腰三角形

查看试题解析
2. 已知Rt△ABC中，∠C=90°，AC=4，BC=6，那么下列各式中，正确的是（）

A、 $sinA = \frac{2}{3}$ B、 $cosA = \frac{2}{3}$ C、 $tanA = \frac{2}{3}$ D、 $cotA = \frac{2}{3}$

查看试题解析
3. 已知 $\vec{a}$ ， $\vec{b}$ 是两个非零向量， $\vec{e}$ 是一个单位向量，下列等式中正确的是（）

A、 $\frac{\vec{a}}{| \vec{a} |} = \vec{e}$ B、 $\frac{\vec{a}}{| \vec{a} |} = \frac{\vec{b}}{| \vec{b} |}$ C、 $| \vec{a} | \vec{e} = \vec{a}$ D、 $| \vec{e} | \vec{a} = \vec{a}$

查看试题解析
4. 已知 $\frac{a}{b} = \frac{3}{5}$ ，下列说法中，错误的是（）

A、 $\frac{a + b}{b} = \frac{8}{5}$ B、 $\frac{a - b}{b} = \frac{- 2}{5}$ C、 $\frac{a + 1}{b + 1} = \frac{a}{b}$ D、 $\frac{b}{a} = \frac{5}{3}$

查看试题解析
5. 如图，在△ABC中，点E、F分别是边AC、BC的中点，设 $\vec{B C}$ = $\underset{a}{\to}$ ， $\vec{C A}$ = $\vec{b}$ ，用 $\underset{a}{\to}$ 、 $\vec{b}$ 表示 $\vec{E F}$ ，下列结果中正确的是（）

A、 $\frac{1}{2} (\vec{a} + \vec{b})$ B、 $- \frac{1}{2} (\vec{a} + \vec{b})$ C、 $\frac{1}{2} (\vec{b} - \vec{a})$ D、 $\frac{1}{2} (\vec{a} - \vec{b})$

查看试题解析
6.
如图，点F是矩形ABCD的边CD上一点，射线BF交AD的延长线于点E，则下列结论错误的是（　　）

A、 $\frac{E D}{E A} = \frac{D F}{A B}$ B、 $\frac{D E}{B C} = \frac{E F}{F B}$ C、 $\frac{B C}{D E} = \frac{B F}{B E}$ D、 $\frac{B F}{B E} = \frac{B C}{A E}$

查看试题解析

二、填空题

7. 已知线段 $a = 4 c m$ ， $b = 9 c m$ ，那么线段 $a$ 、 $b$ 的比例中项等于 $c m$ .

查看试题解析
8. 已知点P是线段AB的黄金分割点，AB=4厘米，则较短线段AP的长是厘米．

查看试题解析
9. 已知两地的实际距离为800米，画在图上的距离（图距）为2厘米，在这样的地图上，图距为16厘米的两地间的实际距离为千米．

查看试题解析
10. 计算： $(2 \vec{a} + \vec{b}) - \frac{1}{2} (6 \vec{a} - 4 \vec{b})$ = ．

查看试题解析
11. 已知△ABC的两条中线AD和BE相交于点G，BG=8，则BE= ．

查看试题解析
12. 在以O为坐标原点的直角坐标平面内有一点A（4，2），如果AO与x轴正半轴的夹角为α，那么cosα= ．

查看试题解析
13. 在△ABC中，∠C=90°，sinA= $\frac{12}{13}$ ， BC=12，那么AC= ．

查看试题解析
14. 如果α是锐角，且cotα=tan25°，那么α=度．

查看试题解析
15. 如图，线段BD与线段CE相交于点A，ED∥BC，已知2BC=3ED，AC=8，则AE= ．

查看试题解析
16. 如图，点C、D在线段AB上（AC＞BD），△PCD是边长为6的等边三角形，且∠APB=120°，若AB=19，则AC= ．

查看试题解析
17. 如果三角形有一边上的高恰好等于这边长的 $\frac{1}{2}$ ，那么称这个三角形为“好玩三角形”，在Rt△ABC是“好玩三角形”，且∠C=90°，则tanA= ．

查看试题解析
18. 在Rt△ABC中，∠ACB=90°，AB=9，cosA= $\frac{2}{3}$ ，如果将△ABC绕着点C旋转至△A′B′C′的位置，使点B′落在∠ACB的角平分线上，A′B′与AC相交于点D，那么线段CD的长等于．

查看试题解析

三、解答题

19. 计算：3sin60°-2cos30°+tan60°•cot45°

查看试题解析
20. 已知：如图，两个不平行的向量 $\vec{a}$ 和 $\vec{b}$ ．（不要求写作法，但要指出图中表示结论的向量）

求作：

(1)、 $2 \vec{a} + \vec{b}$

(2)、 $\vec{a} - \vec{b}$

查看试题解析
21. 如图，在△ABC中，DE∥BC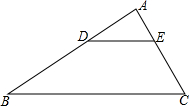， $\frac{DE}{BC}$ = $\frac{2}{5}$ ．

(1)、如果AD=4，求BD的长度；

(2)、如果S_△ADE=2，求S_四边形_DBCE的值．

查看试题解析
22. 如图，在△ABC中，AB=AC=10，sinC= $\frac{3}{5}$ ，点D是BC上一点，且DC=AC．

(1)、求BD的长；

(2)、求tan∠BAD．

查看试题解析
23. 如图，在四边形ABCD中，AD∥BC，BA和CD的延长线交于P，AC和BD交于点O，连接PO并延长分别交AD、BC于M、N．求证：AM=DM．

查看试题解析
24. 如图，已知直线y=- $\frac{3}{4}$ x+b与y轴相交于点B（0，3），与x轴交于点A，将△AOB沿y轴折叠，使点A落在x轴上的点C．

(1)、求点C的坐标；

(2)、设点P为线段CA上的一个动点，点P与点A、C不重合．联结PB．以点P为端点作射线PM交AB于点M，使∠BPM=∠BAC．
①求证：△PBC∽△MPA．

②是否存在点P，使△PBM为直角三角形？若存在，请求出点P的坐标；若不存在，请说明理由．

查看试题解析
25. 在△ABC中，AB=AC=10，sin∠BAC= $\frac{3}{5}$ ，过点C作CD∥AB，点E在边AC上，AE=CD，联结AD，BE的延长线与射线CD、射线AD分别交于点F、G．设CD=x，△CEF的面积为y．

(1)、求证：∠ABE=∠CAD．

(2)、如图，当点G在线段AD上时，求y关于x的函数解析式及定义域．

(3)、若△DFG是直角三角形，求△CEF的面积．

查看试题解析