上海市浦东新区第四教育署2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-08-27 类型:期中考试
一、单选题
-
1. 若ac=bd(ac≠0),则下列比例式中不成立的是( )A、 B、 C、 D、2. 已知:Rt△ABC中,∠C=90°,sinB= , 则tanA等于( )A、 B、 C、 D、3. 如果点D、E分别在△ABC的两边AB、AC上,下列条件中可以推出DE∥BC的是( )A、 , B、 , C、 , D、 ,4. 把△ABC的各边长都增加两倍,则锐角A的正弦值( )A、增加2倍 B、增加4倍 C、不变 D、不能确定5. 已知线段a、b、c,求作线段x,使 ,以下做法正确的是…( )A、
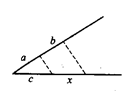 B、
B、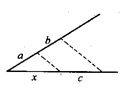 C、
C、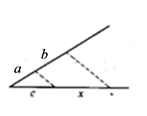 D、
D、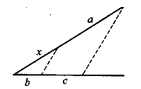 6. 如图,∠ABC=∠CDB=90°,BC=3,AC=5,如果△ABC与△CDB相似,那么BD的长( )
6. 如图,∠ABC=∠CDB=90°,BC=3,AC=5,如果△ABC与△CDB相似,那么BD的长( )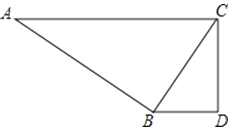 A、 B、 C、 D、或
A、 B、 C、 D、或二、填空题
-
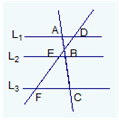
7. 计算: =;8. 在 中, , , , .9. 已知,AB=4,P是AB黄金分割点,PA>PB,则PA的长为 .10. 如图,L1∥L2∥L3 , AB=4,DF=8,BC=6,则DE=.
 11. 如图,DE∥BC,DF=2,FC=4,那么 = .
11. 如图,DE∥BC,DF=2,FC=4,那么 = .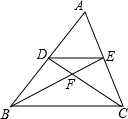 12. 如果在比例尺为1:1 000 000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是千米.
12. 如果在比例尺为1:1 000 000的地图上,A、B两地的图上距离是3.4厘米,那么A、B两地的实际距离是千米.
13. 如果两个相似三角形的面积之比是9:25,其中小三角形一边上的中线长是12cm,那么大三角形对应边上的中线长是cm.14. 已知△ABC中,点D在边BC上,且BD=2D C . 设 , ,那么 等于(结果用 、 表示); 15. 如图,若点G是△ABC的重心,GD∥BC,则 = .
等于(结果用 、 表示); 15. 如图,若点G是△ABC的重心,GD∥BC,则 = . 16. 如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD= ,则△ABC的边长为 .
16. 如图,在等边三角形ABC中,P为BC上一点,D为AC上一点,且∠APD=60°,BP=1,CD= ,则△ABC的边长为 .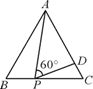 17. 如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是 .
17. 如图,Rt△ABC中,∠C=90°,BC=4,AC=6,现将△ABC沿ED翻折,使点A与点B重合,折痕为DE,则tan∠BED的值是 . 18. 如图,在△ABC中,∠C=90°,AB=10,cosB= ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是 .
18. 如图,在△ABC中,∠C=90°,AB=10,cosB= ,点M是AB边的中点,将△ABC绕着点M旋转,使点C与点A重合,点A与点D重合,点B与点E重合,得到△DEA,且AE交CB于点P,那么线段CP的长是 .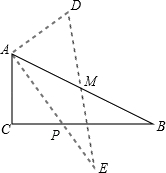
三、解答题
-
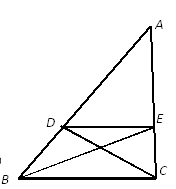
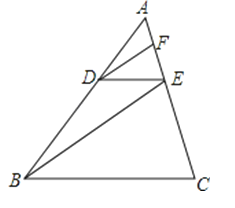
19. 计算:20. 如图,在△ABC中,点D在边AB上,点F、E在边AC上,且DF∥BE, .
求:的值.
 21. 如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC= ,AB=13.
21. 如图,在△ABC中,AB=AC,BD是AC边上的中线,AE⊥BC,垂足为点E,交BD于F,cos∠ABC= ,AB=13.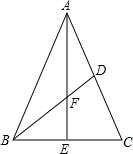 (1)、求AE的长;(2)、求tan∠DBC的值.22. 如图:四边形ABCD对角线AC与BD相交于点O,OD=2OA,OC=2OB.
(1)、求AE的长;(2)、求tan∠DBC的值.22. 如图:四边形ABCD对角线AC与BD相交于点O,OD=2OA,OC=2OB. (1)、求证:△AOB∽△DOC;(2)、点E在线段OC上,若AB∥DE,求证:OD2=OE•OC.
(1)、求证:△AOB∽△DOC;(2)、点E在线段OC上,若AB∥DE,求证:OD2=OE•OC.