山西省吕梁市文水县2017-2018学年九年级上学期数学期中考试试卷

试卷更新日期：2019-08-27 类型：期中考试

进入出卷网下载

一、单选题

1. 已知函数：①y=ax²；②y=3（x﹣1）²+2；③y=（x+3）²﹣2x²；④y= $\frac{1}{x^{2}}$ +x．其中，二次函数的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 一块竹条编织物，先将其按如图所示绕直线MN翻转180°，再将它按逆时针方向旋转90°，所得的竹条编织物是（）

A、 B、 C、 D、

查看试题解析
3. 下列命题中的真命题是（　　　）

A、全等的两个图形是中心对称图形 B、关于中心对称的两个图形全等 C、中心对称图形都是轴对称图形 D、轴对称图形都是中心对称图形

查看试题解析
4. 对于抛物线 $y = - \frac{1}{2} {(x + 1)}^{2} + 3$ ，下列结论：①抛物线的开口向下；②对称轴为直线x=1；③顶点坐标为（－1，3）；④x＞1时，y随x的增大而减小，其中符合题意结论的个数为（）

A、1 B、2 C、3 D、4

查看试题解析
5. 已知二次函数y＝ax²＋bx＋c的y与x的部分对应值如下表：

x

…

－1

0

1

3

…

y

…

－3

1

3

1

…

则下列判断中正确的是（）

A、抛物线开口向上 B、抛物线与y轴交于负半轴 C、当x＝4时，y＞0 D、方程ax²＋bx＋c＝0的正根在3与4之间

查看试题解析
6. 4张扑克牌如图（1）所示放在桌子上，小敏把其中两张旋转180°后得到如图（2）所示，那么她所旋转的牌从左起是（）

A、第一张、第二张 B、第二张、第三张 C、第三张、第四张 D、第四张、第一张

查看试题解析
7. 抛物线 $y = - \frac{1}{2} x^{2} - x$ 的顶点坐标是（）

A、 $(1, - \frac{1}{2})$ B、 $(- 1, \frac{1}{2})$ C、 $(\frac{1}{2}, - 1)$ D、(1，0)

查看试题解析
8. 关于x的一元二次方程x²﹣6x+2k=0有两个不相等的实数根，则实数k的取值范围是（）

A、 $k \leq \frac{9}{2}$ B、 $k < \frac{9}{2}$ C、 $k \geq \frac{9}{2}$ D、 $k > \frac{9}{2}$

查看试题解析
9. 如图，将△ABC绕点C顺时针方向旋转40°得△A’CB’ ，若AC⊥A’B’ ，则∠BAC等于（）

A、50° B、60° C、70° D、80°

查看试题解析
10. 二次函数y=ax²+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞﹣3b；（3）7a﹣3b+2c＞0；（4）若点A（﹣3，y₁）、点B（﹣ $\frac{1}{2}$ ，y₂）、点C（7，y₃）在该函数图象上，则y₁＜y₃＜y₂；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x₁和x₂ ，且x₁＜x₂ ，则x₁＜﹣1＜5＜x₂ ．其中正确的结论有（）

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 三角形两边长分别为3和6，第三边是方程x²﹣13x+36=0的根，则三角形的周长为．

查看试题解析
12. 如图是“靠右侧通道行驶”的交通标志，若将图案绕其中心顺时针旋转90°，则得到的图案是“”的交通标志（不画图案，只填含义）．

查看试题解析
13. 若函数y=（a﹣1）x²﹣4x+2a的图象与x轴有且只有一个交点，则a的值为．

查看试题解析
14. 已知抛物线p：y=ax²+bx+c的顶点为C，与x轴相交于A、B两点（点A在点B左侧），点C关于x轴的对称点为C′，我们称以A为顶点且过点C′，对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线，直线AC′为抛物线p的“梦之星”直线．若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是y=x²+2x+1和y=2x+2，则这条抛物线的解析式为．

查看试题解析

三、解答题

15. 解一元二次方程

(1)、x²﹣2x﹣1=0

(2)、（2x﹣3）²=（x+2）²

查看试题解析
16. 实践与操作：一般地，如果把一个图形绕着一个定点旋转一定角度α（α小于360°）后，能够与原来的图形重合，那么这个图形叫做旋转对称图形，这个定点叫做旋转对称中心，α叫做这个旋转对称图形的一个旋转角，请根据上述规定解答下列问题：

(1)、请写出一个有一个旋转角是90°旋转对称图形，这个图形可以是；

(2)、尺规作图：在图中的等边三角形内部作出一个图形，使作出的图形和这个等边三角形构成的整体既是一个旋转对称图形又是一个轴对称图形（作出的图形用实线，作图过程用虚线，保留痕迹，不写做法）．

查看试题解析
17. 如图，正方形ABCD与正方形A₁B₁C₁D₁关于某点中心对称，已知A，D₁ ， D三点的坐标分别是（0，4），（0，3），（0，2）.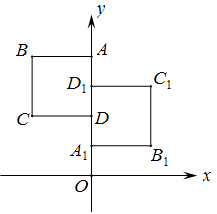

(1)、对称中心的坐标；

(2)、写出顶点B，C，B₁ ， C₁的坐标.

查看试题解析
18. 某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一定的关系．每盆植入3株时，平均单株盈利3元；以同样的栽培条件，若每盆增加1株，平均单株盈利就减少0.5元．要使每盆的盈利达到10元，每盆应该植多少株？

查看试题解析
19. 某公司草坪的护栏是由50段形状相同的抛物线组成的，为牢固起见，每段护栏需按间距0.4m加设不锈钢管（如图）做成立柱，为了计算所需不锈钢管立柱的总长度，设计人员测得如图所示的数据．

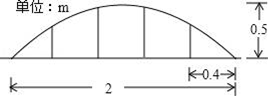(1)、求此抛物线的解析式；

(2)、计算所需不锈钢管的总长度．

查看试题解析
20. 某贸易公司购进“长青”胶州大白菜，进价为每棵20元，物价部门规定其销售单价每棵不得超过80元，也不得低于30元．经调查发现：日均销售量y（棵）与销售单价x（元/棵）满足一次函数关系，并且每棵售价60元时，日均销售90棵；每棵售价30元时，日均销售120棵．

(1)、求日均销售量y与销售单价x的函数关系式；

(2)、在销售过程中，每天还要支出其他费用200元，求销售利润w（元）与销售单价x之间的函数关系式；并求当销售单价为何值时，可获得最大的销售利润？最大销售利润是多少？

查看试题解析
21. 操作：在△ABC中，AC＝BC＝2，∠C＝90°，将一块等腰三角形板的直角顶点放在斜边AB的中点P处，将三角板绕点P旋转，三角板的两直角边分别交射线AC、CB于D、E两点。图①，②，③是旋转三角板得到的图形中的3种情况。研究：

(1)、三角板ABC绕点P旋转，观察线段PD和PE之间有什么数量关系？并结合图②加以证明。

(2)、三角板ABC绕点P旋转，△PBE是否能为等腰三角形？若能，指出所有情况（即写出△PBE为等腰三角形时CE的长）；若不能，请说明理由。（图④不用）

查看试题解析
22.
在平面直角坐标系中，现将一块等腰直角三角板ABC放在第二象限，斜靠在两坐标轴上，且点A（0，2），点C（﹣1，0），如图所示：抛物线y=ax²+ax﹣2经过点B．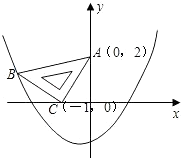

(1)、求点B的坐标；

(2)、求抛物线的解析式；

(3)、在抛物线上是否还存在点P（点B除外），使△ACP仍然是以AC为直角边的等腰直角三角形？若存在，求所有点P的坐标；若不存在，请说明理由．

查看试题解析

x	…	－1	0	1	3	…
y	…	－3	1	3	1	…