山西省临汾市襄汾县2018-2019学年九年级上学期数学期中考试试卷
试卷更新日期:2019-08-27 类型:期中考试
一、单选题
-
1. 如果 ,那么 的值等于( )A、 B、 C、 D、2. 下列等式不成立的是( )A、 B、 =4 C、 D、3. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )
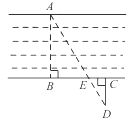 A、60m B、40m C、30m D、20m4. 如图所示,将△ABC的三边分别扩大一倍得到△A1B1C1 , (顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是( )
A、60m B、40m C、30m D、20m4. 如图所示,将△ABC的三边分别扩大一倍得到△A1B1C1 , (顶点均在格点上),它们是以P点为位似中心的位似图形,则P点的坐标是( )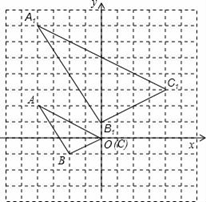 A、(﹣4,﹣3) B、(﹣3,﹣3) C、(﹣4,﹣4) D、(﹣3,﹣4)5. 用配方法解一元二次方程x2﹣2x=1时,此方程可变形为( )A、(x﹣1)2=0 B、(x﹣1)2=1 C、(x﹣1)2=2 D、(x+1)2=26. 在△ABC中,若∠A、∠B满足|cosA﹣ |+(sinB﹣ )2=0,则∠C=( )A、45° B、60° C、75° D、105°7. 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )
A、(﹣4,﹣3) B、(﹣3,﹣3) C、(﹣4,﹣4) D、(﹣3,﹣4)5. 用配方法解一元二次方程x2﹣2x=1时,此方程可变形为( )A、(x﹣1)2=0 B、(x﹣1)2=1 C、(x﹣1)2=2 D、(x+1)2=26. 在△ABC中,若∠A、∠B满足|cosA﹣ |+(sinB﹣ )2=0,则∠C=( )A、45° B、60° C、75° D、105°7. 如图,点E在正方形ABCD的对角线AC上,且EC=2AE,直角三角形FEG的两直角边EF、EG分别交BC、DC于点M、N.若正方形ABCD的边长为a,则重叠部分四边形EMCN的面积为( )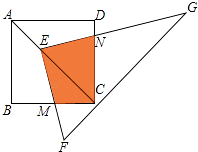 A、 a2 B、 a2 C、 a2 D、 a28. 如图,在直角梯形ABCD中,P是下底BC边上一动点,点E、F、G分别为AB、PE、DP的中点,AB=AD=4,则FG的长为( )
A、 a2 B、 a2 C、 a2 D、 a28. 如图,在直角梯形ABCD中,P是下底BC边上一动点,点E、F、G分别为AB、PE、DP的中点,AB=AD=4,则FG的长为( )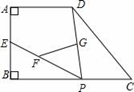 A、2 B、2 C、 D、29. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC= ,AB的垂直平分线ED交BC的延长线于D点,垂足为E , 则sin∠CAD=( )
A、2 B、2 C、 D、29. 如图,在Rt△ABC中,∠ACB=90°,BC=3,AC= ,AB的垂直平分线ED交BC的延长线于D点,垂足为E , 则sin∠CAD=( )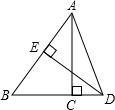 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
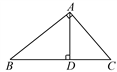
10. 若关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有实数根,则m的取值范围是 .11. 若 的小数部分为m,则代数式m( +3)的值为 .12. 晓明从自家的阳台上观测对面一幢大楼,测得楼顶的仰角为45°,楼底的俯角为30°,如果两楼之间两楼之间的水平距离为30米,那么对面大楼的高为米.13. 如图,Rt△ABC中,∠A=90°,AD⊥BC于点D,若BD∶CD=3∶2,则tan∠B= .
 ,14. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为 .
,14. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为 .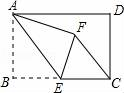
三、解答题
-
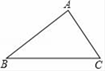
15. 计算:(1)、 ;(2)、﹣12× .16. 解方程:(1)、(x﹣3)(x+1)=﹣3;(2)、x2﹣x﹣1=0.17. 已知a、b、c是△ABC的三边长,且满足 ,a+b+c=12,试判断△ABC的形状.18. 如图,在△ABC中,sinB= ,cosC= ,AB=5,求△ABC的面积.
 19. 如图所示,小杨在广场上的A处正面观测一座楼房墙上的广告屏幕,测得屏幕下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该屏幕上端C处的仰角为45°.若该楼高为26.65m,小杨的眼睛离地面1.65m,广告屏幕的上端与楼房的顶端平齐.求广告屏幕上端与下端之间的距离.( ≈1.732,结果精确到0.1m)
19. 如图所示,小杨在广场上的A处正面观测一座楼房墙上的广告屏幕,测得屏幕下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该屏幕上端C处的仰角为45°.若该楼高为26.65m,小杨的眼睛离地面1.65m,广告屏幕的上端与楼房的顶端平齐.求广告屏幕上端与下端之间的距离.( ≈1.732,结果精确到0.1m)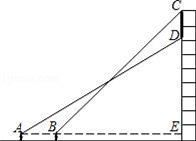 20. 山西历史悠久,人文荟萃,拥有丰厚的历史文化遗产,是全国唯一一个拥有五岳、五镇和四大佛教名山的省份,今年八月份,光明旅行社将五台山一日游的费用,在原来门市报价的基础上每人降价60元,这样某旅行团原定13500元的旅游费用,只花费了10800元.
20. 山西历史悠久,人文荟萃,拥有丰厚的历史文化遗产,是全国唯一一个拥有五岳、五镇和四大佛教名山的省份,今年八月份,光明旅行社将五台山一日游的费用,在原来门市报价的基础上每人降价60元,这样某旅行团原定13500元的旅游费用,只花费了10800元. (1)、求该旅行社五台山一日游的原来门市报价是每人多少元?(2)、为迎接“十一”长假,该旅行社将五台山一日游的费用,在原来门市报价的基础上连续两次降价,降价后每人的费用为192元,求平均每次的降价率.21. 如图,在△ABC中,∠C=90°,AC=8cm , BC=6cm , 点P从点A沿AC向C以2cm/s的速度移动,到C即停,点Q从点C沿CB向B以1cm/s的速度移动,到B就停.
(1)、求该旅行社五台山一日游的原来门市报价是每人多少元?(2)、为迎接“十一”长假,该旅行社将五台山一日游的费用,在原来门市报价的基础上连续两次降价,降价后每人的费用为192元,求平均每次的降价率.21. 如图,在△ABC中,∠C=90°,AC=8cm , BC=6cm , 点P从点A沿AC向C以2cm/s的速度移动,到C即停,点Q从点C沿CB向B以1cm/s的速度移动,到B就停.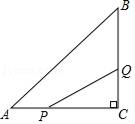 (1)、若P、Q同时出发,经过几秒钟S△PCQ=2cm2;(2)、若点Q从C点出发2s后点P从点A出发,再经过几秒△PCQ与△ACB相似.22. 情景观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示,将将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.
(1)、若P、Q同时出发,经过几秒钟S△PCQ=2cm2;(2)、若点Q从C点出发2s后点P从点A出发,再经过几秒△PCQ与△ACB相似.22. 情景观察:将矩形ABCD纸片沿对角线AC剪开,得到△ABC和△A′C′D,如图1所示,将将△A′C′D的顶点A′与点A重合,并绕点A按逆时针方向旋转,使点D、A(A′)、B在同一条直线上,如图2所示.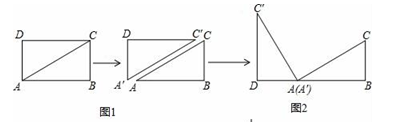
 (1)、观察图2可知:与BC相等的线段是 , ∠CAC′=°;
(1)、观察图2可知:与BC相等的线段是 , ∠CAC′=°;
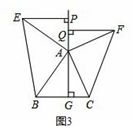
(2)、问题探究:如图3,△ABC中,AG⊥BC于点G,以A为直角顶点,分别以AB、AC为直角边,向△ABC外作等腰Rt△ABE和等腰Rt△ACF,过点E、F作射线GA的垂线,垂足分别为P、Q.试探究EP与FQ之间的数量关系,并证明你的结论.(3)、拓展延伸:如图4,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作矩形ABME和矩形ACNF,射线GA交EF于点H,若AB=kAE、AC=kAF,探究HE与HF之间的数量关系,并说明理由.