内蒙古自治区鄂尔多斯市准格尔旗2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-08-27 类型：期中考试
一、单选题
-
1. 在以下绿色食品、回收、节能、节水四个标志中，是轴对称图形的是（ ）
A.
B.
C.
D.
A、A B、B C、C D、D2. 人字梯中间一般会设计一“拉杆”，这样做的道理是（ ）
A、两点之间，线段最短 B、垂线段最短 C、三角形具有稳定性 D、两直线平行，内错角相等3. 以下列各组线段为边，能组成三角形的是（ ）A、1cm，2cm，4cm B、2cm，3cm，6cm C、12cm，5cm，6cm D、8cm，6cm，4cm4. 为增强学生体质，感受中国的传统文化，学校将国家级非物质文化遗产--“抖空竹”引入阳光特色大课间 下面左图是某同学“抖空竹”时的一个瞬间，小聪把它抽象成右图的数学问题：已知 ， ， ，则 的度数是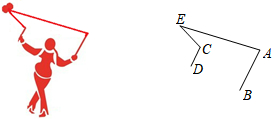
A、 B、 C、 D、5. 如图，△ABC≌△EBD，AB=4cm，BD=7cm，则CE的长度为（ ）
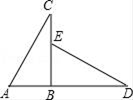A、1cm B、2cm C、3cm D、4cm6. 下列说法中错误的是（ ）A、三角形的中线、角平分线、高线都是线段 B、任意三角形的外角和都是360° C、有一个内角是直角的三角形是直角三角形 D、三角形的一个外角大于任何一个内角7. 如图，在△ABC中，BD为△ABC的角平分线，CE为△ABC的高，CE、BD交于点F，∠A=50°，∠BCA=60°，那么∠BFC的度数是（ ）
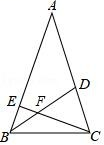A、115° B、120° C、125° D、130°8. 如图，等边三角形ABC中，AD⊥BC，垂足为D，点E在线段AD上，∠EBC=45°，则∠ACE等于（ ）
A、15° B、30° C、45° D、60°9. 如图，△ABC的面积为12cm2 ， 点D在BC边上，E是AD的中点，则△BCE的面积是（ ）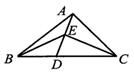
A、4cm2 B、6cm2 C、8cm2 D、10cm210. 如图，在△ABC中，AB=AC，∠A=36°，AC的垂直平分线交AB于E，D为垂足，连接EC，若CE=5，则BC等于（ ）
A、2 B、3 C、4 D、5二、填空题
-
11. 若正多边形的每一个内角为 ，则这个正多边形的边数是 ．12. 如图4×5的方格纸中，在除阴影之外的方格中任意选择一个涂黑，与图中阴影部分构成轴对称图形的涂法有 种．
13. 如图，四边形ABCD的对角线AC、BD相交于点O，△ABO≌△ADO.下列结论：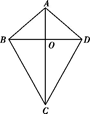
①AC⊥BD；②CB=CD；③△ABC≌△ADC；④DA=DC.其中所有正确结论的序号是.
14. 如图，△ABC中，AB=AC，∠BAC和∠ACB的平分线相交于点D，∠ADC=125°，那么∠CAB的大小是度．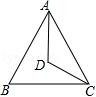
15. 如图，在△ABC中，AC＝8，BC＝5，AB的垂直平分线DE交AB于点D，交边AC于点E，则△BCE的周长为 ．
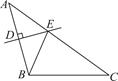16. 如图所示， 中， ，BD是角平分线， ，垂足是E， ， ，则DE的长为cm．
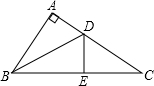17. 如图，点D是∠ABC内一点，点B在射线BA上，且∠DBE=∠BDE=15°，DE∥BC，过点D作DF⊥BC，垂足为点F，若BE=10，则DF= ．
18. 如图，AF ， AD分别是△ABC的高和角平分线，且∠B＝32°，∠C＝78°，则∠DAF＝ ．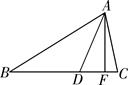
19. 如图：∠ABC=∠DEF，AB=DE，要证明△ABC≌△DEF，需要添加一个条件为（只添加一个条件即可）；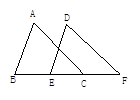
三、解答题
-
20. 作图题：如图，在平面直角坐标系xOy中，A（2，3），B（3，1），C（﹣2，﹣1）．
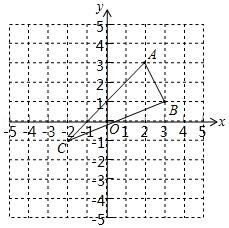
①在图中作出△ABC关于x轴的对称图形△A1B1C1并写出A1 ， B1 ， C1的坐标；
②在y轴上画出点P，使PA+PB最小．（不写作法，保留作图痕迹）
③求△ABC的面积．
21. 如图，l1、l2交于A点，P、Q的位置如图所示，试确定M点，使它到l1、l2的距离相等，且到P、Q两点的距离也相等．（用直尺和圆规）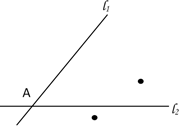
22. 如图，已知点A，B，C，D在同一条直线上，AB=DC，AF=DE，CF=BE．求证：BF=CE．
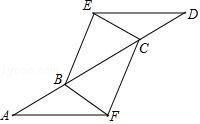23. 如图，△ABC中，AB=AC，AD⊥BC，CE⊥AB，AE=CE．求证：
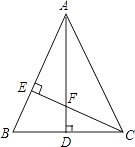(1)、△AEF≌△CEB；(2)、AF=2CD．24. 如图，已知某船于上午8时在A处观测小岛C在北偏东60°方向上，该船以每小时20海里的速度向东航行到B处，测得小岛C在北偏东30°方向上，船以原来的速度继续向东航行2小时，到达岛C正南方点D处，船从A到D一共航行了多少海里？
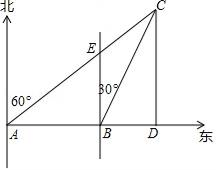25. 问题情境：如图①，在直角三角形ABC中，∠BAC= ，AD⊥BC于点D，可知：∠BAD=∠C（不需要证明）；
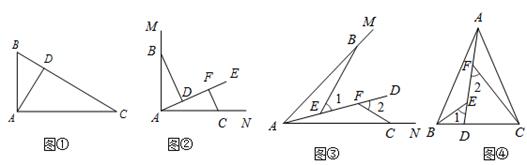(1)、特例探究：如图②，∠MAN=90°，射线AE在这个角的内部，点B、C在∠MAN的边AM、AN上，且AB="AC，"CF⊥AE于点F，BD⊥AE于点D.证明：△ABD≌△CAF；
(2)、归纳证明：如图③，点B，C在∠MAN的边AM、AN上，点E，F在∠MAN内部的射线AD上，∠1、∠2分别是△ABE、△CAF的外角.已知AB=AC，∠1=∠2=∠BA C．求证：△ABE≌△CAF；(3)、拓展应用：如图④，在△ABC中，AB=AC，AB＞BC.点D在边BC上，CD=2BD，点E、F在线段AD上，∠1=∠2=∠BA
C.若△ABC的面积为15，则△ACF与△BDE的面积之和为.