内蒙古乌海市海南区2018-2019学年八年级上学期数学期中考试试卷
试卷更新日期：2019-08-27 类型：期中考试
一、单选题
-
1. 下列图形是轴对称图形的有（ ）
A、2个 B、3个 C、4个 D、5个2. 下面各组线段中，能组成三角形的是（ ）A、5，11，6 B、8，8，16 C、10，5，4 D、6，9，143. 等腰三角形的一个角是50°，则它的底角是（ ）A、50° B、50°或65° C、80° D、65°4. 和点P（2，﹣5）关于x轴对称的点是（ ）A、（﹣2，﹣5） B、（2，﹣5） C、（2，5） D、（﹣2，5）5. 在△ABC中，∠B=∠C ， 与△ABC全等的三角形有一个角是120°，那么在△ABC中与这个120°的角对应相等的角是（ ）A、∠A B、∠B C、∠C D、∠B或∠C6. 下列各式从左到右的变形，正确的是（ ）．A、－x－y=－(x－y) B、－a+b=－(a+b) C、(y-x)2=(x-y)2 D、(a-b)3=(b-a)37. 若（x+k）（x﹣5）的积中不含有x的一次项，则k的值是（ ）
A、0 B、5 C、﹣5 D、﹣5或58. 如图，∠DAE=∠ADE=15°，DE∥AB，DF⊥AB，若AE=8，则DF等于（ ）
A、5 B、4 C、3 D、29. 已知∠AOB ， 求作射线OC ， 使OC平分∠AOB ， 那么作法的合理顺序是（ ）
①作射线OC；②在射线OA和OB上分别截取OD、OE ， 使OD=OE；
③分别以D、E为圆心，大于 DE的长为半径在∠AOB内作弧，两弧交于点C ．
A、①②③ B、②①③ C、②③① D、③①②10. n边形的每个外角都为24°，则边数n为（ ）A、13 B、14 C、15 D、1611. 下列两个三角形中，一定全等的是（ ）A、有一个角是40°，腰相等的两个等腰三角形 B、两个等边三角形 C、有一个角是100°，底相等的两个等腰三角形 D、有一条边相等，有一个内角相等的两个等腰三角形12. 如图，直线a、b、c表示互相交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的站址有（ ）
A、一处 B、二处 C、三处 D、四处二、填空题
-
13. 计算：（﹣2xy2）2•3x2y•（﹣x3y4）= ．14. 把3555 ， 4444 ， 5333由小到大用＜连接为 ．15. 已知△ABC≌△DEF，且△ABC的周长为12，若AB=3，EF=4，则AC= ．16.
如图，点P在∠AOB的平分线上，若使△AOP≌△BOP，则需添加的一个条件是 （只写一个即可，不添加辅助线）．
17. 已知等腰三角形的两边长分别是4和9，则周长是 ．18. 如图：在△ABC中，AB=3cm ， AC=4cm ， 则BC边上的中线AD的取值范围是 ．
19. 如图所示，∠A+∠B+∠C+∠D+∠E= ．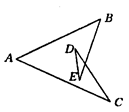
20. 如图，在△ABC中，AB＝8，BC＝6，AC的垂直平分线MN交AB、AC于点M、N，则△BCM的周长为.
三、解答题
-
21.(1)、先化简，再求值x（x﹣1）+2x（x+1）﹣（3x﹣1）（2x﹣5），其中x=2．(2)、解方程（3x﹣2）（2x﹣3）=（6x+5）（x﹣1）+15．22. 如图，点E、F在BC上，BE＝CF，AB＝DC，∠B＝∠C．求证：∠A＝∠D．
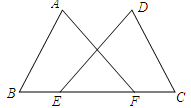23. 如图，∠A=∠B ， CE∥DA ， CE交AB于E ． 求证：△CEB是等腰三角形．
24. 如图，在等边△ABC中，点D，E分别在边BC，AB上，且BD=AE，AD与CE交于点F．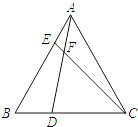
(1)、求证：AD=CE；(2)、求∠DFC的度数．25. 已知：如图，AD平分∠BAC ， DE⊥AB ， DF⊥AC ， DB=DC ，求证：BE=FC ．
26. 如图①，在△ABC中，D、E分别是AB、AC上的点，AB=AC ， AD=AE ， 然后将△ADE绕点A顺时针旋转一定角度，连接BD ， CE ， 得到图②，将BD、CE分别延长至M、N ， 使DM= BD ， EN= CE ， 得到图③，请解答下列问题：
(1)、在图②中，BD与CE的数量关系是；(2)、在图③中，猜想AM与AN的数量关系，∠MAN与∠BAC的数量关系，并证明你的猜想．27. 如图，在矩形ABCD中，AB＝12厘米，BC＝6厘米，点P沿AB边从点A开始向点B以2厘米/秒的速度移动，点Q沿DA边从点D开始向点A以1厘米/秒的速度移动，如果点P、Q同时出发，用t（秒）表示移动的时间（0≤t≤6）．
(1)、当PB＝2厘米时，求点P移动多少秒？(2)、t为何值时，△PAQ为等腰直角三角形？(3)、求四边形QAPC的面积，并探究一个与计算结果有关的结论．