山西省太原市2018-2019学年七年级上学期数学期中考试试卷
试卷更新日期:2019-08-27 类型:期中考试
一、单选题
-
1. ﹣5的相反数是( )A、 B、﹣ C、5 D、﹣52. 2018年7月份,我国居民消费价格同比上涨2.1%,记作+2.1%,其中水产品价格下降0.4%,应记作( )A、0.4% B、﹣0.4% C、0.4 D、﹣0.43. 某几何体由大小相同的小立方块搭成,从上面看这个几何体的形状如图所示(小正方形中的数字表示该位置的小立方块的个数).从左面看该几何体的形状图是( )
 A、
A、 B、
B、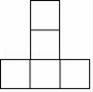 C、
C、 D、
D、 4. 我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(﹣4)的过程.按照这种方法,图2表示的过程是在计算( )
4. 我国是最早认识负数,并进行相关运算的国家.在古代数学名著《九章算术》里,就记载了利用算筹实施“正负术”的方法,图1表示的是计算3+(﹣4)的过程.按照这种方法,图2表示的过程是在计算( )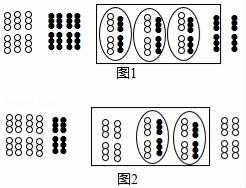 A、(﹣4)+(﹣2) B、(﹣4)+2 C、4+(﹣2) D、4+25. 下列运算正确的是( )A、(﹣1)2018=﹣1 B、32=3×2=6 C、(﹣1)×(﹣3)=3 D、﹣3﹣2=﹣16. 经党中央批准、国务院批复自2018年起,将每年秋分日设立为“中国农民丰收节”.据国家统计局数据显示,2018年我省夏粮总产量达到2299000吨,将数据“2299000吨”用科学记数法表示为( )A、229.9×104吨 B、2.299×106吨 C、22.99×105吨 D、2299×103吨7.
A、(﹣4)+(﹣2) B、(﹣4)+2 C、4+(﹣2) D、4+25. 下列运算正确的是( )A、(﹣1)2018=﹣1 B、32=3×2=6 C、(﹣1)×(﹣3)=3 D、﹣3﹣2=﹣16. 经党中央批准、国务院批复自2018年起,将每年秋分日设立为“中国农民丰收节”.据国家统计局数据显示,2018年我省夏粮总产量达到2299000吨,将数据“2299000吨”用科学记数法表示为( )A、229.9×104吨 B、2.299×106吨 C、22.99×105吨 D、2299×103吨7.用一平面去截如图5个几何体,能得到长方形截面的几何体的个数是( )
 A、4 B、3 C、2 D、18. 下列计算正确的是( )A、3a+2b=5ab B、5a2﹣3a2=2 C、3﹣2(a﹣2b)=3﹣2a+2b D、2a2b﹣5a2b=﹣3a2b9. 如图是一个长方体之和表面展开图,纸片厚度忽略不计,按图中数据,这个盒子容积为( )
A、4 B、3 C、2 D、18. 下列计算正确的是( )A、3a+2b=5ab B、5a2﹣3a2=2 C、3﹣2(a﹣2b)=3﹣2a+2b D、2a2b﹣5a2b=﹣3a2b9. 如图是一个长方体之和表面展开图,纸片厚度忽略不计,按图中数据,这个盒子容积为( )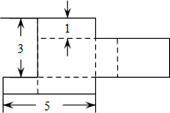 A、6 B、8 C、10 D、1510. 某地气象资料表明,高度毎増加1000m,气温就降低大约6℃.现在地面气温是t℃,则hm高空的气温用含h,t的代数式表示正确的是( )A、t+6h B、t﹣6h C、t﹣ D、t﹣
A、6 B、8 C、10 D、1510. 某地气象资料表明,高度毎増加1000m,气温就降低大约6℃.现在地面气温是t℃,则hm高空的气温用含h,t的代数式表示正确的是( )A、t+6h B、t﹣6h C、t﹣ D、t﹣二、填空题
-
11. 化简﹣3x﹣5x的结果为12. 太原市2018年2月份某一周内毎天的最高气温与最低气温记录如下表:
星期
一
二
三
四
五
六
日
最高气温
4℃
5℃
3℃
4℃
3℃
﹣2℃
﹣2℃
最低气温
﹣13℃
﹣13℃
﹣13℃
﹣9℃
﹣11℃
﹣13℃
﹣15℃
则这周内温差最大的一天是星期 .
13. 下列各式是按新定义的已知“△”运算得到的,观察下列等式:2△5=2×3+5=11,2△(﹣1)=2×3+(﹣1)=5,
6△3=6×3+3=21,4△(﹣3)=4×3+(﹣3)=9……
根据这个定义,计算(﹣2018)△2018的结果为
14. 根据流程图中的程序,当输入数值x为﹣8吋,输出的数值y为 . 15. 用火柴棒按如图方式拼图,第1个图形共用3根火柴棒,第2个图形共用9根火柴棒,第3个图形共用18根火柴棒,……按照这样的方式继续拼图,第n个图形共用根火柴棒.(用含n的代数式表示)
15. 用火柴棒按如图方式拼图,第1个图形共用3根火柴棒,第2个图形共用9根火柴棒,第3个图形共用18根火柴棒,……按照这样的方式继续拼图,第n个图形共用根火柴棒.(用含n的代数式表示)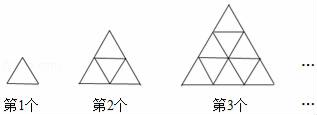
三、解答题
-
16. 计算:(1)、﹣10﹣(﹣18)+(﹣4)(2)、(﹣54)÷(﹣3)+ ×(﹣ )(3)、( )×(﹣24)(4)、(﹣ )3+[﹣8﹣(﹣3)×2]÷417. 计算:﹣8x2+3x﹣2与10x2﹣6x的和.18. 随着中国快递行业整体规模的迅速壮大,分拣机器人系统的应用也呈现智能化、自动化的发展趋势.每台分拣机器人一小时可以分拣1.8万件包裹,大大提高了分拣效率.某分拣仓库计划平均每天分拣20万件包裹,但实际每天分拣量与计划相比有出入,下表是该仓库10月份第一周分拣包裹的情况(超过计划量记为正、未达计划量记为负):
星期
一
二
三
四
五
六
日
分拣情况(单位:万件)
+6
﹣3
﹣4
+5
﹣1
+7
﹣8
(1)、该仓库本周内分拣包裹数量最多的一天是星期 , 最少的一天是星期 , 最多的一天比最少的一天多分拣了万件包裹;(2)、该仓库本周实际分拣包裹一共多少万件?19. 先化简,再求值:3a2b﹣6ab2﹣2(2a2b﹣3ab2﹣2),其中a=﹣1.b=2.20. 观察下面由8个小立方块组成的图形,请在指定的位置画出从正面、左面、上面看到的这个几何体的形状图.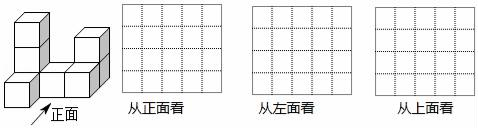 21. 某体育用品商店硝售一种乒乓球拍和兵兵球,乒乓球拍每副定价75元,乒乓球毎盒定价10元.“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
21. 某体育用品商店硝售一种乒乓球拍和兵兵球,乒乓球拍每副定价75元,乒乓球毎盒定价10元.“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.方案一:买一副乒乓球拍送一盒兵兵球;
方案二:乒乓球拍和乒乓球都按定价的90%付款.
某客户要到该体育用品商店购买乒乓球拍10副,兵兵球x盒(x>10).
(1)、若该客户按方案一购买,需付款元;若该客户按方案二购买,需付款元;(用含x的代数式表示)(2)、若x=30,通过计算说明此时按哪种方案购买较为合算.22. 综合与实践问题情境:在棱长为1的正方体右侧拼搭若干个棱长小于或等于1的其它正方体,使拼成的立体图形为一个长方体.如图1,是两个棱长为1的正方体搭成的长方体,图2是从上面看这个长方体得到的平面图形,它由两个正方形组成.

操作探究:
(1)、如图3是在棱长为1的正方体右侧拼搭了4个棱长小于1的正方体形成的长方体,请画出从上面看这个长方体得到的平面图形;(2)、已知一个长方体是按上述方式拼成的,组成它的正方体约10个,且若从上面看这个长方体得到的平面图形由4个正方形组成.请从A,B两题中任选一题作答,我选择哪题.
A.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形)
B.请画出从上面看这个长方体得到的平面图形.(请画出所有可能的图形,并在所画图形的下方直接写出拼成该长方体所需的正方体的总个数)
23. 综合与探究阅读材料:
数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.例如,两个有理数在数轴上对应的点之间的距离可以用这两个数的差的绝对值表示;
在数轴上,有理数3与1对应的两点之间的距离为|3﹣1|=2;
在数轴上,有理数5与﹣2对应的两点之间的距离为|5﹣(﹣2)|=7;
在数轴上,有理数﹣2与3对应的两点之间的距离为|﹣2﹣3|=5;
在数轴上,有理数﹣8与﹣5对应的两点之间的距离为|﹣8﹣(﹣5)|=3;……
如图1,在数轴上有理数a对应的点为点A,有理数b对应的点为点B,A,B两点之间的距离表示为|a﹣b|或|b﹣a|,记为|AB|=|a﹣b|=|b﹣a|.

解决问题:
(1)、数轴上有理数﹣10与﹣5对应的两点之间的距离等于;数轴上有理数x与﹣5对应的两点之间的距离用含x的式子表示为;若数轴上有理数x与﹣1对应的两点A,B之间的距离|AB|=2,则x等于;(2)、联系拓广:如图2,点M,N,P是数轴上的三点,点M表示的数为4,点N表示的数为﹣2,动点P表示的数为x.
请从A,B两题中任选一题作答,我选择题.

A.①若点P在点M,N两点之间,则|PM|+|PN|=;
②若|PM|=2|PN|,即点P到点M的距离等于点P到点N的距离的2倍,则x等于 .
B.①若点P在点M,N之间,则|x+2|+|x﹣4|=;
若|x+2|+|x﹣4|═10,则x=;
②根据阅读材料及上述各题的解答方法,|x+2|+|x|+|x﹣2|+|x﹣4|的最小值等于 .