2017年四川省泸州市中考数学试卷
试卷更新日期:2017-06-26 类型:中考真卷
一、选择题
-
1. ﹣7的绝对值是( )A、7 B、﹣7 C、 D、﹣2. “五一”期间,某市共接待海内外游客约567000人次,将567000用科学记数法表示为( )A、567×103 B、56.7×104 C、5.67×105 D、0.567×1063. 下列各式计算正确的是( )A、2x•3x=6x B、3x﹣2x=x C、(2x)2=4x D、6x÷2x=3x4. 如图是一个由4个相同的正方体组成的立体图形,它的左视图是( )
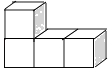 A、
A、 B、
B、 C、
C、 D、
D、 5. 已知点A(a,1)与点B(﹣4,b)关于原点对称,则a+b的值为( )A、5 B、﹣5 C、3 D、﹣36. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )
5. 已知点A(a,1)与点B(﹣4,b)关于原点对称,则a+b的值为( )A、5 B、﹣5 C、3 D、﹣36. 如图,AB是⊙O的直径,弦CD⊥AB于点E.若AB=8,AE=1,则弦CD的长是( )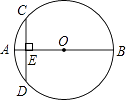 A、 B、2 C、6 D、87. 下列命题是真命题的是( )A、四边都是相等的四边形是矩形 B、菱形的对角线相等 C、对角线互相垂直的平行四边形是正方形 D、对角线相等的平行四边形是矩形8. 下列曲线中不能表示y与x的函数的是( )A、
A、 B、2 C、6 D、87. 下列命题是真命题的是( )A、四边都是相等的四边形是矩形 B、菱形的对角线相等 C、对角线互相垂直的平行四边形是正方形 D、对角线相等的平行四边形是矩形8. 下列曲线中不能表示y与x的函数的是( )A、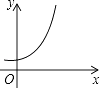 B、
B、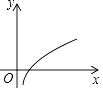 C、
C、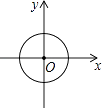 D、
D、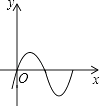 9. 已知三角形的三边长分别为a、b、c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式S= ,其中p= ;我国南宋时期数学家秦九韶(约1202﹣1261)曾提出利用三角形的三边求其面积的秦九韶公式S= ,若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、10. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )
9. 已知三角形的三边长分别为a、b、c,求其面积问题,中外数学家曾经进行过深入研究,古希腊的几何学家海伦(Heron,约公元50年)给出求其面积的海伦公式S= ,其中p= ;我国南宋时期数学家秦九韶(约1202﹣1261)曾提出利用三角形的三边求其面积的秦九韶公式S= ,若一个三角形的三边长分别为2,3,4,则其面积是( )A、 B、 C、 D、10. 如图,在矩形ABCD中,点E是边BC的中点,AE⊥BD,垂足为F,则tan∠BDE的值是( )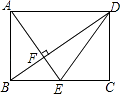 A、 B、 C、 D、11. 已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( )
A、 B、 C、 D、11. 已知抛物线y= x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ,3),P是抛物线y= x2+1上一个动点,则△PMF周长的最小值是( )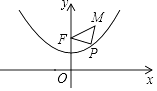 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
12. 在一个不透明的袋子中装有4个红球和2个白球,这些球除了颜色外无其他差别,从袋子中随机摸出一个球,则摸出白球的概率是 .13. 分解因式:2m2﹣8= .14. 若关于x的分式方程 + =3的解为正实数,则实数m的取值范围是 .15. 在△ABC中,已知BD和CE分别是边AC、AB上的中线,且BD⊥CE,垂足为O.若OD=2cm,OE=4cm,则线段AO的长度为 cm.
三、解答题
-
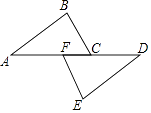
16. 计算:(﹣3)2+20170﹣ ×sin45°.17. 如图,点A、F、C、D在同一条直线上,已知AF=DC,∠A=∠D,BC∥EF,求证:AB=DE.
 18. 化简: •(1+ )19. 某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
18. 化简: •(1+ )19. 某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A、B、C、D、E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题: (1)、补全条形统计图;(2)、求这30名职工捐书本数的平均数、众数和中位数;(3)、估计该单位750名职工共捐书多少本?20. 某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.(1)、甲、乙两种书柜每个的价格分别是多少元?(2)、若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.21. 如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.
(1)、补全条形统计图;(2)、求这30名职工捐书本数的平均数、众数和中位数;(3)、估计该单位750名职工共捐书多少本?20. 某中学为打造书香校园,计划购进甲、乙两种规格的书柜放置新购进的图书,调查发现,若购买甲种书柜3个、乙种书柜2个,共需资金1020元;若购买甲种书柜4个,乙种书柜3个,共需资金1440元.(1)、甲、乙两种书柜每个的价格分别是多少元?(2)、若该校计划购进这两种规格的书柜共20个,其中乙种书柜的数量不少于甲种书柜的数量,学校至多能够提供资金4320元,请设计几种购买方案供这个学校选择.21. 如图,海中一渔船在A处且与小岛C相距70nmile,若该渔船由西向东航行30nmile到达B处,此时测得小岛C位于B的北偏东30°方向上;求该渔船此时与小岛C之间的距离.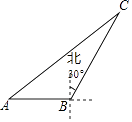 22. 一次函数y=kx+b(k≠0)的图象经过点A(2,﹣6),且与反比例函数y=﹣ 的图象交于点B(a,4)(1)、求一次函数的解析式;(2)、将直线AB向上平移10个单位后得到直线l:y1=k1x+b1(k1≠0),l与反比例函数y2= 的图象相交,求使y1<y2成立的x的取值范围.23. 如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.
22. 一次函数y=kx+b(k≠0)的图象经过点A(2,﹣6),且与反比例函数y=﹣ 的图象交于点B(a,4)(1)、求一次函数的解析式;(2)、将直线AB向上平移10个单位后得到直线l:y1=k1x+b1(k1≠0),l与反比例函数y2= 的图象相交,求使y1<y2成立的x的取值范围.23. 如图,⊙O与Rt△ABC的直角边AC和斜边AB分别相切于点C、D,与边BC相交于点F,OA与CD相交于点E,连接FE并延长交AC边于点G.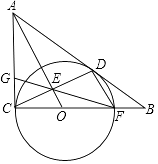 (1)、求证:DF∥AO;(2)、若AC=6,AB=10,求CG的长.24.
(1)、求证:DF∥AO;(2)、若AC=6,AB=10,求CG的长.24.如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(﹣1,0)、B(4,0)、C(0,2)三点.
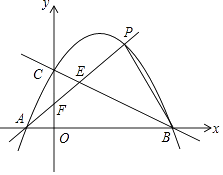 (1)、求该二次函数的解析式;(2)、点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;(3)、点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2 , 求S1﹣S2的最大值.
(1)、求该二次函数的解析式;(2)、点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;(3)、点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2 , 求S1﹣S2的最大值.