云南省昆明市官渡区2018-2019学年七年级下学期数学期末考试试卷

试卷更新日期：2019-08-27 类型：期末考试

进入出卷网下载

一、填空题(每小题3分，共24分)

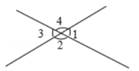
1. 4是的算术平方根．

查看试题解析
2. 把方程2x-y=3改写成用含x的式子表示y的形式，得y= 。

查看试题解析
3. 如图，两条直线相交成四个角，已知∠2=3∠1，那么∠4=度。

查看试题解析
4. 点A的坐标（4，-3），它到x轴的距离为

查看试题解析
5. 某小区五月份1日至5日每天用水量变化情况如图所示，那么这5天中用水量最多的一天比最少的一天多吨。

查看试题解析
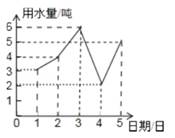6. 如图所示，要在一条公路的两侧铺设平行管道，已知一侧铺设的角度为61°34′，为使管道对接，另一侧铺设的角度为。

查看试题解析
7. 关于x、y的二元一次方程组 ${\begin{cases} 2 x + y = 2 m + 1 \\ x + 2 y = 3 \end{cases}$ 的解满足不等式x-y＞4，则m的取值范围是。

查看试题解析
8. 已知AB∥x轴，点A的坐标为(2，-1)，并且AB=3，则点B的坐标为。

查看试题解析

二、选择题(每小题3分，共27分)

9. 下列图形可由平移得到的是（）

A、 B、 C、 D、

查看试题解析
10. 以下问题，不适合用全面调查的是（）

A、了解全班同学每周体育锻炼的时间 B、旅客上飞机前的安检 C、学校招聘教师，对应聘人员面试 D、了解全市中小学生每天的零花钱

查看试题解析
11. 下列实数中，无理数是（）

A、 $\frac{22}{7}$ B、 $\sqrt{9}$ C、 $\frac{π}{3}$ D、3.14159265

查看试题解析
12. 根据下列表述，能确定具体位置的是（）

A、官渡古镇南 B、东经116°北纬42° C、北偏西30° D、电影院

查看试题解析
13. 若a>b，则下列不等式错误的是（）

A、a-5>b-5 B、5a>5b C、 $\frac{a}{5}$ ＞ $\frac{b}{5}$ D、5-a＞5-b

查看试题解析
14. 下列命题属于真命题的是（）

A、同旁内角相等，两直线平行 B、相等的角是对顶角 C、平行于同一条直线的两条直线平行 D、同位角相等

查看试题解析
15. 如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠AOM=35°，则∠CON的度数为（）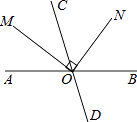

A、35° B、45° C、55° D、65°

查看试题解析
16. 估计 $\sqrt{29}$ 的值在两个整数（）

A、3与4之间 B、5与6之间 C、6与7之间 D、3与10之间

查看试题解析
17. 利用两块相同的长方体木块测量一张桌子的高度．首先按图①方式放置，再交换两木块的位置，按图②方式放置．测量的数据如图，则桌子的高度是（）

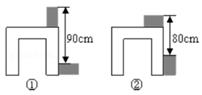A、84cm B、85cm C、86cm D、87cm

查看试题解析

三、解答题(共69分)

18. 计算：

(1)、 $3 (\sqrt{2} - 1) - 2 (\sqrt{2} + \sqrt{\frac{1}{4}})$

(2)、 ${}^{3}{\sqrt{- 8}} + \sqrt{{(- 3)}^{2}} + \sqrt{3} - | 1 - \sqrt{3} |$

查看试题解析
19. 解下列方程组：

(1)、 ${\begin{array}{l} x = 1 - 3 y, \\ 3 x - y = 3; \end{array}$

(2)、 ${\begin{array}{l} 3 x - 4 y = 9, \\ 2 x - 3 y = 7. \end{array}$

查看试题解析
20. x取哪些整数值时，不等式5x-17<8(x-1)与x-5≤ $\frac{x - 8}{2}$ 都成立?

查看试题解析
21. 如图，在平面直角坐标系xOy中，△ABC三个顶点的坐标分别为(-2，-2)，(3，1)，(0，2)，若把△ABC向上平移3个单位长度，再向左平移1个单位长度得到△ABC，点A，B，C的对应点分别为A'，B'，C'

(1)、在图中画出平移后的△A'B'C'，并写出点A'，B'，C'的坐标；

(2)、求△A'B'C'的面积

查看试题解析
22. 已知2a-1的算术平方根是3，3a+b+4的立方根是2，求a-b的平方根。

查看试题解析
23. 如图，直线EF分别与直线AB、CD相交于点P和点Q，已知：AB∥CD，∠1=∠2，求证：PG∥QH。证明：因为AB∥CD(已知)
所以∠APQ=∠ （）

因为∠1=∠2（已知）

所以∠APQ-∠1=∠-∠ (等式的性质)

所以∠GPQ=∠

所以P∥QH()

查看试题解析
24. 2019年6月6日，工信部正式向四家电信企业发放5G商用牌照，标志着5G元年开始华为公司作为5G行业的领军者，已经具备从芯片、产品到系统组网的世界领先的5G技术，是全球唯一家能够提供端到端50商用解决方案的通讯企业为了了解某中学学生对5G通讯技术的了解情况，随机抽取部分学生进行问卷，将是分成“非常了解”、“比较了解”、“一般了解”、“不了解“四种类型，分别记为A、B、C、D根据调查结果绘制了如下尚不完整的两个统计图。

(1)、本次问卷共随机调查了名学生，在扇形统计图中m= ．”B”所在扇形的圆心角的度数为度；

(2)、请根据数据信息补全条形统计图；

(3)、若该校有2000名学生，估计选择“非常了解”，“比较了解”的学生共约有多少人？

查看试题解析
25. 平行线问题的探索

(1)、问题一：
已知：如图，AB∥CD，EF⊥AB于点O，FG交CD于点P，当∠1=30°时，求∠EFG的度数。

甲、乙、丙三位同学用不同的方法添加辅助线解决问题，如图1：
甲同学辅助线的做法和分析思路如下
辅助线：（）
分析思路
①欲求∠EFG的度数，由图可知只需转化为求∠2和∠3的度数；
②由MN∥CD可知，∠2=∠1，又由已知∠1的度数可得∠2的度数；
③由AB∥CD，MN〃CD推出AB∥MN，由此可推出∠3=∠4；
④由已知EF⊥AB，可得∠4=90°，所以可得∠3的度数；
⑤从而可求∠EFG的度数
Ⅰ.请你根据乙同学所画的图形，描述乙同学辅助线的做法
辅助线：；
Ⅱ.请你根据丙同学所画的图形，且不再添加其他辅助线，求∠EFG的度数

(2)、问题二
如图2，在平面直角坐标系中，点A为x轴负半轴上一点，点B为x轴正半轴上一点，C(0，a)，D(b，a)，其中a，b满足关系式：|a+3|+(b-a+1)²=0．

①a= ，b= ；
②根据已知点的坐标判断AB与CD的位置关系是。

查看试题解析

26. 某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇，如表是近两周的销售情况：

销售时段	销售数量		销售收入
销售时段	A种型号	B种型号	销售收入
第一周	3台	4台	1200元
第二周	5台	6台	1900元

(进价、售价均保持不变，利润=销售收入-进货成本)

(1)、求A、B两种型号的电风扇的销售单价；

(2)、若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台?

(3)、在(2)的条件下，超市销售完这50台电风扇能否实现利润超过1850元的目标?若能，请给出相应的采购方案；若不能，请说明理由。

查看试题解析