云南省红河州2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-08-27 类型:期末考试
一、填空题(本大题共6个小题,每小题3分,共18分)
-
1. 已知y=2xm-2+3是一次函数,则m= 。
2. 分解因式:a3-2a2+a= 。3. 如图,在▱ABCD中,对角线AC和BD交于点O,点E为AB边上的中点,OE=2.5cm,则AD=cm。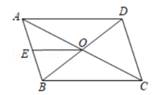 4. 若二次根式 有意义,则x的取值范围是 .5. 如图所示,有一块直角三角形纸片,∠C=90°,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则BD的长为。
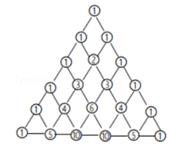
4. 若二次根式 有意义,则x的取值范围是 .5. 如图所示,有一块直角三角形纸片,∠C=90°,AC=8cm,BC=6cm,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则BD的长为。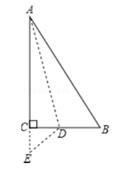 6. 我国古代数学领域有些研究成果曾位居世界前列,其中“杨辉三角”就是一例.南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用图中的三角形解释二项式和的乘方规律.杨辉三角两腰上的数都是1,其余每个数都为它的上方(左右)两数之和,这个三角形给出了(a+b)n(n=1,2,3,4,5)的展开式(按a的次数由大到小的顺序)的系数规律.例如,此三角形中第3行的3个数1,2,1,恰好对应着(a+b)2=a2+2ab+b2展开式中各项的系数:第4行的4个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中各项的系数,等等.利用上面呈现的规律填空:
6. 我国古代数学领域有些研究成果曾位居世界前列,其中“杨辉三角”就是一例.南宋数学家杨辉(约13世纪)所著的《详解九章算术》(1261年)一书中,用图中的三角形解释二项式和的乘方规律.杨辉三角两腰上的数都是1,其余每个数都为它的上方(左右)两数之和,这个三角形给出了(a+b)n(n=1,2,3,4,5)的展开式(按a的次数由大到小的顺序)的系数规律.例如,此三角形中第3行的3个数1,2,1,恰好对应着(a+b)2=a2+2ab+b2展开式中各项的系数:第4行的4个数1,3,3,1,恰好对应着(a+b)3=a3+3a2b+3ab2+b2展开式中各项的系数,等等.利用上面呈现的规律填空:(a+b)6=a6+6a5b+ +20a3b3+15a2b4+ +b6
二、选择题(本大题共8个小题,每小题4分,共32分)
-
7. 下面四个图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 8. 下列根式中,最简二次根式是( )A、 B、 C、 D、9. 正六边形的每个内角度数为( )A、90° B、108° C、120° D、150°10. 下列运算正确的是( )A、7a+2b=9ab B、(-3a3b)2=6a9b2 C、(a+b)2=a2+b2 D、11. 平行四边形、矩形、菱形、正方形都具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直平分且相等12. 某居民小区10户家庭5月份的用水情况统计结果如表所示:
8. 下列根式中,最简二次根式是( )A、 B、 C、 D、9. 正六边形的每个内角度数为( )A、90° B、108° C、120° D、150°10. 下列运算正确的是( )A、7a+2b=9ab B、(-3a3b)2=6a9b2 C、(a+b)2=a2+b2 D、11. 平行四边形、矩形、菱形、正方形都具有的性质是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线互相垂直平分且相等12. 某居民小区10户家庭5月份的用水情况统计结果如表所示:月用水量/m3
4
5
6
8
9
户数
2
3
3
1
1
这10户家庭的月平均用水量是( )
A、2m3 B、3.2m3 C、5.8m3 D、6.4m313. 如图,四边形ABCD是正方形,延长BA到点E,使BE=BD,则∠ADE等于( )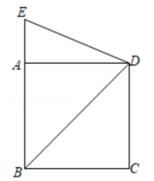 A、15.5° B、22.5° C、45° D、67.5°14. 已知直线y=kx+k-3在平面直角坐标系中的位置大致如图所示,则k的取值范围是( )。
A、15.5° B、22.5° C、45° D、67.5°14. 已知直线y=kx+k-3在平面直角坐标系中的位置大致如图所示,则k的取值范围是( )。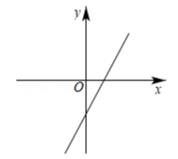 A、k>0 B、0<k<3 C、k>3 D、k<0
A、k>0 B、0<k<3 C、k>3 D、k<0三、解答题(本大题共9个小题,共70分)
-
15. 计算:
2-2+ ( -1)-( π-2019)0-
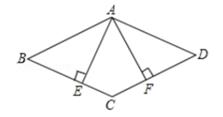
16. 如图,已知四边形ABCD是平行四边形,AE⊥BC,AF⊥DC,垂足分别是E,F,并且BE=DF。求证;四边形ABCD是菱形。
 17. 某市建设全长540米的绿化带,有甲、乙两个工程队参加.甲队平均每天绿化的长度是乙队的1.5倍.若由一个工程队单独完成绿化,乙队比甲队多用6天,分别求出甲、乙两队平均每天绿化的长度。18. 如图,已知直线y= x+2交x轴于点A,交y轴于点B,
17. 某市建设全长540米的绿化带,有甲、乙两个工程队参加.甲队平均每天绿化的长度是乙队的1.5倍.若由一个工程队单独完成绿化,乙队比甲队多用6天,分别求出甲、乙两队平均每天绿化的长度。18. 如图,已知直线y= x+2交x轴于点A,交y轴于点B, (1)、求A,B两点的坐标;(2)、已知点C是线段AB上的一点,当S△AOC= S△AOB时,求直线OC的解析式。19. 在边长为1的小正方形组成的正方形网格中,建立如图所示的平面直角坐标系,已知△ABC的三个顶点都在格点上。
(1)、求A,B两点的坐标;(2)、已知点C是线段AB上的一点,当S△AOC= S△AOB时,求直线OC的解析式。19. 在边长为1的小正方形组成的正方形网格中,建立如图所示的平面直角坐标系,已知△ABC的三个顶点都在格点上。 (1)、请作出△ABC关于x轴对称的△A′B′C′,并分别写出点A′,B′,C′的坐标。(2)、在格点上是否存在一点D,使A,B,C,D四点为顶点的四边形是平行四边形,若存在,直接写出D点的坐标(只需写出一点即可)。20. 如图,在边长12的正方形ABCD中,点E是CD的中点,点F在边AD上,且AF=3DF,连接BE,BF,EF,请判断△BEF的形状,并说明理由。
(1)、请作出△ABC关于x轴对称的△A′B′C′,并分别写出点A′,B′,C′的坐标。(2)、在格点上是否存在一点D,使A,B,C,D四点为顶点的四边形是平行四边形,若存在,直接写出D点的坐标(只需写出一点即可)。20. 如图,在边长12的正方形ABCD中,点E是CD的中点,点F在边AD上,且AF=3DF,连接BE,BF,EF,请判断△BEF的形状,并说明理由。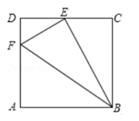 21. 某中学为了解该校学生的体育锻炼情况,随机抽查了该校部分学生一周的体育锻炼时间的情况,并绘制了如下两幅不完整的统计图:
21. 某中学为了解该校学生的体育锻炼情况,随机抽查了该校部分学生一周的体育锻炼时间的情况,并绘制了如下两幅不完整的统计图: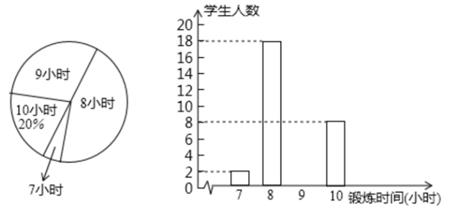
根据以上信息解答以下问题:
(1)、本次抽查的学生共有多少名,并补全条形统计图;(2)、写出被抽查学生的体育锻炼时间的众数和中位数;(3)、该校一共有1800名学生,请估计该校学生一周体育锻炼时间不低于9小时的人数.22. 学校为了更新体育器材,计划购买足球和篮球共100个,经市场调查:购买2个足球和5个篮球共需600元;购买3个足球和1个篮球共需380元。(1)、请分别求出足球和篮球的单价;(2)、学校去采购时恰逢商场做促销活动,所有商品打九折,并且学校要求购买足球的数量不少于篮球数量的3倍,设购买足球a个,购买费用W元。①写出W关于a的函数关系式,
②设计一种实际购买费用最少的方案,并求出最少费用。
23. 如图,在Rt△ABC中,∠C=90°,∠A=45°,AC=10cm,点D从点A出发沿AC方向以1cm/s的速度向点C匀速运动,同时点E从点B出发沿BA方向以 cm/s的速度向点A匀速运动,当其中一个点到达终点时,另一个点也随之停止运动,设点D,E运动的时间是t(0<1≤10)s.过点E作EF⊥BC于点F,连接DE,DF。 (1)、用含t的式子填空:BE= cm ,CD= cm。(2)、试说明,无论t为何值,四边形ADEF都是平行四边形;(3)、当t为何值时,△DEF为直角三角形?请说明理由。
(1)、用含t的式子填空:BE= cm ,CD= cm。(2)、试说明,无论t为何值,四边形ADEF都是平行四边形;(3)、当t为何值时,△DEF为直角三角形?请说明理由。