广西玉林市陆川县2018-2019学年八年级下学期数学期末考试试卷
试卷更新日期:2019-08-27 类型:期末考试
一、选择题:(本题共12小题,每小题3分,共36分).
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 下列等式正确的是( )A、 B、 C、 D、3. 以下列数组为边长中,能构成直角三角形的是( )A、6,7,8 B、0.2,0.3,0.5 C、1,1, D、 , ,4. 在平行四边形ABCD中,∠A:∠B:∠C:∠D的可能情况是( )A、2:7:2:7 B、2:2:7:7 C、2:7:7:2 D、2:3:4:55. 关于特殊四边形对角线的性质,矩形具备而平行四边形不一定具备的是( )A、对角线互相平分 B、对角线互相垂直 C、对角线相等 D、对角线平分一组对角6. 正方形的一条对角线长为4,则这个正方形的面积是( )A、8 B、4 C、8 D、167. 函数y=kx+b(k,b为常数k不为0)的图象如图所示,则关于x的不等式kx+b<0的解集是( )
 A、x>2 B、x<0 C、x<1 D、x>18. 若一组数据-1,0,2,4,x的极差为7,则x的值是( )A、-3 B、6 C、7 D、6或-39. 13名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前6名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )A、 方差 B、众数 C、平均数 D、中位数10. 对于函数y=-2x+1,下列结论正确的是( )A、它的图象必经过点(-1,3) B、它的图象经过第一、二、三象限 C、当x> 时,y>0 D、y值随x值的增大而增大11. 在同一直角坐标系中,一次函数y=(k-2)x+k的图象与正比例函数y=kx图象的位置可能是( )A、
A、x>2 B、x<0 C、x<1 D、x>18. 若一组数据-1,0,2,4,x的极差为7,则x的值是( )A、-3 B、6 C、7 D、6或-39. 13名同学参加歌咏比赛,他们的预赛成绩各不相同,现取其中前6名参加决赛,小红同学在知道自己成绩的情况下,要判断自己能否进入决赛,还需要知道这13名同学成绩的( )A、 方差 B、众数 C、平均数 D、中位数10. 对于函数y=-2x+1,下列结论正确的是( )A、它的图象必经过点(-1,3) B、它的图象经过第一、二、三象限 C、当x> 时,y>0 D、y值随x值的增大而增大11. 在同一直角坐标系中,一次函数y=(k-2)x+k的图象与正比例函数y=kx图象的位置可能是( )A、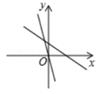 B、
B、 C、
C、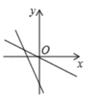 D、
D、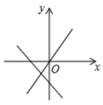 12. 如图,过点A0(1,0)作x轴的垂线,交直线l:y=2x于B1 , 在x轴上取点A1 , 使OA1=OB1 , 过点A1作x轴的垂线,交直线l于B2 , 在x轴上取点A2 , 使OA2=OB2 , 过点A2作x轴的垂线,交直线l于B3 , …,这样依次作图,则点B8的纵坐标为( )
12. 如图,过点A0(1,0)作x轴的垂线,交直线l:y=2x于B1 , 在x轴上取点A1 , 使OA1=OB1 , 过点A1作x轴的垂线,交直线l于B2 , 在x轴上取点A2 , 使OA2=OB2 , 过点A2作x轴的垂线,交直线l于B3 , …,这样依次作图,则点B8的纵坐标为( )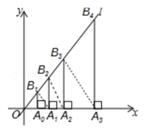 A、( )7 B、2( )7 C、2( )8 D、( )9
A、( )7 B、2( )7 C、2( )8 D、( )9二、填空题:(本大题6小题,每小题3分,共18分,)
-
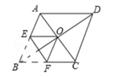
13. 若 有意义,则字母x的取值范围是 .14. 一组数据2,3,3,1,5的众数是 。15. 一次函数y=kx-2的函数值y随自变量x的增大而减小,则k的取值范围是 。16. 某商场利用“五一”开展促销活动:一次性购买某品牌服装3件,每件仅售80元,如果超过3件,则超出部分可享受8折优惠,顾客所付款y(元)与所购服装x(x≥3)件之间的函数解析式为 。17. 如图,菱形ABCD的对角线相交于点O,AC=2,BD=2 ,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形 AEFCD的周长为 。
 18. 如图,一次函数y= x+2的图象与x轴、y轴分别交于点A、B,将△AOB沿直线AB翻折得到△ACB,连接OC,那么线段OC的长为。
18. 如图,一次函数y= x+2的图象与x轴、y轴分别交于点A、B,将△AOB沿直线AB翻折得到△ACB,连接OC,那么线段OC的长为。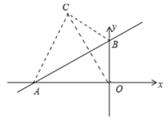
三、解答题:(本大题共8小题,共66分)
-
19. 计算(1)、(2)、20. 已知△ABC的三边长a、b、c满足| a-4|+(2b-12)2+ =0,试判断△ABC的形状,并说明理由.21. 函数y=(m-2)x+m2-4(m为常数)(1)、当m取何值时,y是x的正比例函数?(2)、当m取何值时,y是x的一次函数?22. 某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示:
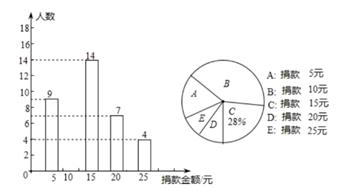 (1)、本次共抽查学生人,并将条形图补充完整;(2)、捐款金额的众数是 ,平均数是 , 中位数为 。(3)、在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?23. 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D
(1)、本次共抽查学生人,并将条形图补充完整;(2)、捐款金额的众数是 ,平均数是 , 中位数为 。(3)、在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?23. 如图,已知一次函数y=kx+b的图象经过A(-2,-1),B(1,3)两点,并且交x轴于点C,交y轴于点D
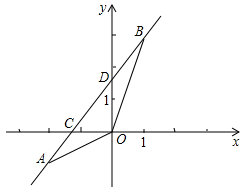 (1)、求该一次函数的解析式;(2)、求△AOB的面积24. 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF。
(1)、求该一次函数的解析式;(2)、求△AOB的面积24. 如图,矩形ABCD的对角线AC,BD相交于点O,点E,F在BD上,BE=DF。 (1)、求证:AE=CF;(2)、若AB=6,∠COD=60°,求矩形ABCD的面积。25. 我市某游乐场在暑假期间推出学生个人门票优惠活动,各类门票价格如下表
(1)、求证:AE=CF;(2)、若AB=6,∠COD=60°,求矩形ABCD的面积。25. 我市某游乐场在暑假期间推出学生个人门票优惠活动,各类门票价格如下表票价种类
(A)夜场票
(B)日通票
(C)节假日通票
单价(元)
80
120
150
某慈善单位欲购买三种类型的门票共100张奖励品学兼优的留守学生,设购买A种票x张,B种票张数是A种票的3倍还多7张,C种票y张,根据以上信息解答下列问题
(1)、直接写出x与y之间的函数关系式;(2)、设购票总费用为W元,求W(元)与x(张)之间的函数关系式(3)、为方便学生游玩,计划购买学生的夜场票不低于20张,且节假日通票至少购买5张,有哪几种购票方案?哪种方案费用最少?26. 如图,把矩形OABC放入平面直角坐标系xOy中,使OA、OC分别落在x、y轴的正半轴上,其中AB=10,对角线AC所在直线解析式为y=- x+b将矩形OABC沿着BE折叠,使点A落在边OC上的点D处 (1)、求点B的坐标;(2)、求EA的长度(3)、点P是y轴上一动点,是否存在点P使得△PBE的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由
(1)、求点B的坐标;(2)、求EA的长度(3)、点P是y轴上一动点,是否存在点P使得△PBE的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由