广西贵港市港南区2018-2019学年七年级下学期数学期末考试试卷
试卷更新日期：2019-08-27 类型：期末考试
一、选择题：(本大题共12小题，每小题3分，共36分．)
-
1. 下列是二元一次方程的是（ ）A、x+8y=0 B、2x2=y C、y+ =0 D、3x=102. 下面四个美术字中，可以看作是轴对称图形的是（ ）A、
B、
C、
D、
3. 下面生活中的实例，不是旋转的是（ ）A、传送带传送货物 B、螺旋桨的运动 C、风车风轮的运动 D、自行车车轮的运动4. 若k为任意整数，且993-99能被k整除，则k不可能是（ ）A、100 B、99 C、98 D、975. 将数字“6”旋转180°，得到数字“9”，将数字“9”旋转180°，得到数字“6”，现将数字“69”旋转180°，得到的数字是（ ）A、96 B、69 C、66 D、996. 计算( )2019．( )2020的结果是（ ）A、 B、 C、 D、7. 一组数据：1，3，6，1，3，1，2，这组数据的众数和中位数分别是（ ）A、1和1 B、1和3 C、2和3 D、1和28. 已知x=3y+5，且x2-7xy+9y2=24，则x2y-3xy2的值为（ ）A、0 B、1 C、5 D、129. 下列条件不能判定AB∥CD的是（ ）
A、∠3=∠4 B、∠1=∠5 C、∠1+∠2=180° D、∠3=∠510. 如图所示，直线a、b、C、d的位置如图所示，若∠1=115°，∠2=115°，∠3=124°，则∠4的度数为（ ）
A、56° B、60° C、65° D、66°11. 如图，在平面内，把矩形ABCD沿EF对折，若∠1=40°，则∠AEF等于（ ）
A、115° B、110° C、120° D、65°12. 已知：如图，点E，F分别在直线AB，CD上，点G，H在两直线之间，线段EF与GH相交于点O，且有∠AEF+∠CFE=180°，∠AEF-∠1=∠2，则在图中相等的角共有（ ）
A、5对 B、6对 C、7对 D、8对二、填空题(本大题共6小题，每小题3分，共18分)
-
13. 化简(x-1)(x+1)的结果是。14. |x-1|+(y-2)2=0，则x-y= 。15. 如图，AB∥CD，EP平分∠BEF，FP平分∠DFE，则∠P= 。
16.如图，10块相同的小长方形墙砖拼成一个大长方形，设小长方形墙砖的长和宽分别为x厘米和y厘米，则列出的方程组为 ．
17. 如图，两个正方形的边长分别为4，3，两阴影部分的面积分别为a，b(a>b)，则a-b等于。
18. 请看杨辉三角(1)，并观察下列等式(2)
根据前面各式的规律，则(a+b)6= 。
三、解答题：(本大题共8小题，满分66分)
-
19.
(1)、因式分解：-3ma2+12ma-9m(2)、解方程组20. 画出△AOB关于点O对称的图形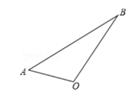
21. 已知a+b=3，ab=2，求代数式a3b+2a2b2+ab3的值22. 甲乙两名运动员进行射击选拔赛，每人射击10次，其中射击中靶情况如下表：第一次
第二次
第三次
第四次
第五次
第六次
第七次
第八次
第九次
第十次
甲
7
10
8
10
9
9
10
8
10
9
乙
10
7
10
9
9
10
8
10
7
10
(1)、选手甲的成绩的中位数是 分；选手乙的成绩的众数是分。(2)、计算选手甲的平均成绩和方差；(3)、已知选手乙的成绩的方差是1.4，则成绩较稳定的是哪位选手?(直按写出结果)23. 为奖励优秀学生，某校准备购买一批文具袋和圆规作为奖品，已知购买1个文具袋和2个圆规需21元，购买2个文具袋和3个圆规需39元。(1)、求文具袋和圆规的单价：(2)、学校准备购买文具袋20个，圆规若干，文具店给出两种优惠方案方案一：购买一个文具袋还送1个圆规
方案二：购买圆规10个以上时，超出10个的部分按原价的八折优惠，文具袋不打折．
①设购买圆规m个(m≥20)，则选择方案一的总费用为 ，选择方案二的总费用为 。
②若学校购买圆规100个，则选择哪种方案更合算？请说明理由 24.如图，CD⊥AB于D，点F是BC上任意一点，FE⊥AB于E，且∠1=∠2，∠3=80°．
(1)、试证明∠B=∠ADG；(2)、求∠BCA的度数．25. 上数学课时，王老师在讲完乘法公式(a±b)2=a2±2ab+b2的多种运用后，要求同学们运用所学知识解答：求代数式x2+4x+5的最小值?同学们经过交流、讨论，最后总结出如下解答方法：解：x2+4x+5=x2+4x+4+1=(x+2)2+1
∵(x+2)2≥0
∴当x=-2时，(x+2)2的值最小，最小值是0，
∴(x+2)2+1≥1
∴当(x+2)2=0时，(x+2)2+1的值最小，最小值是1，
∴x2+4x+5的最小值是1．
请你根据上述方法，解答下列各题
(1)、知识再现：当x=时，代数式x2-6x+12的最小值是；(2)、知识运用：若y=-x2+2x-3，当x=时，y有最值（填“大”或“小”）(3)、知识拓展：若-x2+3x+y+5=0，求y+x的最小值26. 已知直线l1∥l2 ， 直线l3和直线l1、l2交于点C和D，点P是直线l3上一动点
(1)、如图1，当点P在线段CD上运动时，∠PAC，∠APB，∠PBD之间存在什么数量关系?请你猜想结论并说明理由．(2)、当点P在C、D两点的外侧运动时(P点与点C、D不重合，如图2和图3)，上述(1)中的结论是否还成立?若不成立，请直接写出∠PAC，∠APB，∠PBD之间的数量关系，不必写理由．