2017年山东省临沂市中考数学试卷
试卷更新日期:2017-06-26 类型:中考真卷
一、选择题
-
1. ﹣ 的相反数是( )A、 B、﹣ C、2017 D、﹣2017
-
2.
如图,将直尺与含30°角的三角尺摆放在一起,若∠1=20°,则∠2的度数是( )
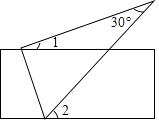 A、50° B、60° C、70° D、80°
A、50° B、60° C、70° D、80° -
3. 下列计算正确的是( )A、﹣(a﹣b)=﹣a﹣b B、a2+a2=a4 C、a2•a3=a6 D、(ab2)2=a2b4
-
4. 不等式组 中,不等式①和②的解集在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、
-
5. 如图所示的几何体是由五个小正方体组成的,它的左视图是( )
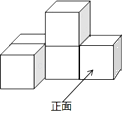 A、
A、 B、
B、 C、
C、 D、
D、
-
6. 小明和小华玩“石头、剪子、布”的游戏,若随机出手一次,则小华获胜的概率是( )A、 B、 C、 D、
-
7. 一个多边形的内角和是外角和的2倍,则这个多边形是( )A、四边形 B、五边形 C、六边形 D、八边形
-
8. 甲、乙二人做某种机械零件,已知甲每小时比乙多做6个,甲做90个所用时间与乙做60个所用时间相等,求甲、乙每小时各做零件多少个.如果设乙每小时做x个,那么所列方程是( )A、 = B、 = C、 = D、 =
-
9. 某公司有15名员工,他们所在部门及相应每人所创年利润如下表所示:
部门
人数
每人创年利润(万元)
A
1
10
B
3
8
C
7
5
D
4
3
这15名员工每人所创年利润的众数、中位数分别是( )
A、10,5 B、7,8 C、5,6.5 D、5,5 -
10. 如图,AB是⊙O的直径,BT是⊙O的切线,若∠ATB=45°,AB=2,则阴影部分的面积是( )
 A、2 B、 ﹣ π C、1 D、 + π
A、2 B、 ﹣ π C、1 D、 + π -
11.
将一些相同的“○”按如图所示摆放,观察每个图形中的“○”的个数,若第n个图形中“○”的个数是78,则n的值是( )
 A、11 B、12 C、13 D、14
A、11 B、12 C、13 D、14 -
12. 在△ABC中,点D是边BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交AB,AC于E,F两点,下列说法正确的是()
 A、若AD⊥BC,则四边形AEDF是矩形 B、若AD垂直平分BC,则四边形AEDF是矩形 C、若BD=CD,则四边形AEDF是菱形 D、若AD平分∠BAC,则四边形AEDF是菱形
A、若AD⊥BC,则四边形AEDF是矩形 B、若AD垂直平分BC,则四边形AEDF是矩形 C、若BD=CD,则四边形AEDF是菱形 D、若AD平分∠BAC,则四边形AEDF是菱形 -
13. 足球运动员将足球沿与地面成一定角度的方向踢出,足球飞行的路线是一条抛物线,不考虑空气阻力,足球距离地面的高度h(单位:m)与足球被踢出后经过的时间t(单位:s)之间的关系如下表:
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论:①足球距离地面的最大高度为20m;②足球飞行路线的对称轴是直线t= ;③足球被踢出9s时落地;④足球被踢出1.5s时,距离地面的高度是11m,其中正确结论的个数是( )
A、1 B、2 C、3 D、4 -
14.
如图,在平面直角坐标系中,反比例函数y= (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
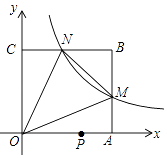 A、6 B、10 C、2 D、2
A、6 B、10 C、2 D、2
二、填空题
-
15. 分解因式:m3﹣9m= .
-
16. 已知AB∥CD,AD与BC相交于点O.若 = ,AD=10,则AO= .

-
17. 计算: ÷(x﹣ )= .
-
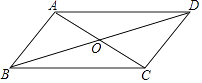
18. 在▱ABCD中,对角线AC,BD相交于点O,若AB=4,BD=10,sin∠BDC= ,则▱ABCD的面积是 .
-
19. 在平面直角坐标系中,如果点P坐标为(m,n),向量 可以用点P的坐标表示为 =(m,n).
已知: =(x1 , y1), =(x2 , y2),如果x1•x2+y1•y2=0,那么 与 互相垂直,下列四组向量:
① =(2,1), =(﹣1,2);
② =(cos30°,tan45°), =(1,sin60°);
③ =( ﹣ ,﹣2), =( + , );
④ =(π0 , 2), =(2,﹣1).
其中互相垂直的是(填上所有正确答案的符号).
三、解答题
-
20. 计算:|1﹣ |+2cos45°﹣ +( )﹣1 .
-
21. 为了解某校学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况,随机抽取了x名学生进行调查统计(要求每名学生选出并且只能选出一个自己最喜爱的节目),并将调查结果绘制成如下统计图表:

学生最喜爱的节目人数统计表
节目
人数(名)
百分比
最强大脑
5
10%
朗读者
15
b%
中国诗词大会
a
40%
出彩中国人
10
20%
根据以上提供的信息,解答下列问题:
(1)、x= , a= , b=;(2)、补全上面的条形统计图;(3)、若该校共有学生1000名,根据抽样调查结果,估计该校最喜爱《中国诗词大会》节目的学生有多少名. -
22.
如图,两座建筑物的水平距离BC=30m,从A点测得D点的俯角α为30°,测得C点的俯角β为60°,求这两座建筑物的高度.

-
23. 如图,∠BAC的平分线交△ABC的外接圆于点D,∠ABC的平分线交AD于点E,
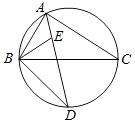 (1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径.
(1)、求证:DE=DB;(2)、若∠BAC=90°,BD=4,求△ABC外接圆的半径. -
24. 某市为节约水资源,制定了新的居民用水收费标准,按照新标准,用户每月缴纳的水费y(元)与每月用水量x(m3)之间的关系如图所示.
 (1)、求y关于x的函数解析式;(2)、若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3?
(1)、求y关于x的函数解析式;(2)、若某用户二、三月份共用水40cm3(二月份用水量不超过25cm3),缴纳水费79.8元,则该用户二、三月份的用水量各是多少m3? -
25.
数学课上,张老师出示了问题:如图1,AC,BD是四边形ABCD的对角线,若∠ACB=∠ACD=∠ABD=∠ADB=60°,则线段BC,CD,AC三者之间有何等量关系?
经过思考,小明展示了一种正确的思路:如图2,延长CB到E,使BE=CD,连接AE,证得△ABE≌△ADC,从而容易证明△ACE是等边三角形,故AC=CE,所以AC=BC+CD.
小亮展示了另一种正确的思路:如图3,将△ABC绕着点A逆时针旋转60°,使AB与AD重合,从而容易证明△ACF是等边三角形,故AC=CF,所以AC=BC+CD.
在此基础上,同学们作了进一步的研究:
 (1)、小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)、小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明.
(1)、小颖提出:如图4,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=45°”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小颖提出的问题,请你写出结论,并给出证明.(2)、小华提出:如图5,如果把“∠ACB=∠ACD=∠ABD=∠ADB=60°”改为“∠ACB=∠ACD=∠ABD=∠ADB=α”,其它条件不变,那么线段BC,CD,AC三者之间有何等量关系?针对小华提出的问题,请你写出结论,不用证明. -
26.
如图,抛物线y=ax2+bx﹣3经过点A(2,﹣3),与x轴负半轴交于点B,与y轴交于点C,且OC=3OB.
 (1)、求抛物线的解析式;(2)、点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)、点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点D在y轴上,且∠BDO=∠BAC,求点D的坐标;(3)、点M在抛物线上,点N在抛物线的对称轴上,是否存在以点A,B,M,N为顶点的四边形是平行四边形?若存在,求出所有符合条件的点M的坐标;若不存在,请说明理由.
