山东省潍坊市2018-2019学年第高二下学期数学期中考试试卷
试卷更新日期:2019-08-27 类型:期中考试
一、选择题:本大题共12小题,每小题5分,共60分.
-
1. 将2封信随意投入3个邮箱,不同的投法有( )A、3种 B、6种 C、8种 D、9种2. 已知函数f(x)=sinx-cosx,则f'( )=( )A、 B、 C、 D、3. 设随机变量x~B(12, ),则D(X)=( )A、 B、 C、 D、34. 已知C8m=C82m-1 , 则m等于( )A、1 B、4 C、1或3 D、3或45. 两名男生和两名女生站成一排照相,则两名男生相邻的概率为( )A、 B、 C、 D、6. 已知函数y=f(x)的图象如图所示,则它的导函数y=f'(x)的图象可以是( )
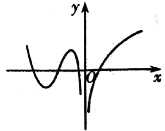 A、
A、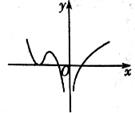 B、
B、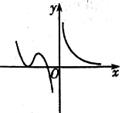 C、
C、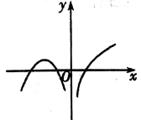 D、
D、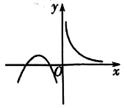 7. 某机构为研究学生玩电脑游戏和对待作业量的态度之间的关系,随机抽取了200名学生进行调查,所得数据如下表所示:
7. 某机构为研究学生玩电脑游戏和对待作业量的态度之间的关系,随机抽取了200名学生进行调查,所得数据如下表所示:认为作业多
认为作业不多
总计
喜欢玩电脑游戏
80
40
120
不喜欢玩电脑游戏
20
60
80
总计
100
100
200
(参考公式: ,可能用到数据:P( =6.635)=0.01,P( =3.841)=0.05),参照以上公式和数据,得到的正确结论是( )
A、有95%的把握认为喜欢玩电脑游戏与认为作业多少有关 B、有95%的把握认为喜欢玩电脑游戏与认为作业多少无关 C、有99%的把握认为喜欢玩电脑游戏与认为作业多少有关 D、有99%的把握认为喜欢玩电脑游戏与认为作业多少无关8. 袋中有三个红球,两个蓝球,现每次摸出一个球,不放回地摸取两次,则在第一次摸到蓝球的条件下,第二次摸到红球的概率为( )A、 B、 C、 D、9. 由数字0,1,2,3,4,5组成的奇偶数字相间且无重复数字的六位数的个数是( )A、60 B、48 C、36 D、2410. 若函数f(x)=ex-ax-b在R上有小于0的极值点,则实数a的取值范围是( )A、(-1,0) B、(0,1) C、(-∞,-1) D、(1,+∞)11. 杨辉是中国南宋时期的一位杰出数学家、教育家,杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关,其中蕴藏了许多优美的规律.如图,在由二项式系数所构成的杨辉三角中,按从上到下、从左到右的顺序,把第1个1记为(1,1),第2个1记为(2,1),第3个1记为(2,2),第4个1记为(3,1),第5个1记为(3,2)…,依次类推,则第31个1应记为( ) A、(15,2) B、(16,1) C、(16,2) D、(17,1)12. 已知函数f(x)=ax2+(a-1)lnx+1(a<u),设A,B为函数f(x)图象上的任意两点,若直线AB的斜率的绝对值不小于2,则实数a的取值范围是( )A、(-∞, ] B、[ ,0) C、(-∞, ] D、[ ,0)
A、(15,2) B、(16,1) C、(16,2) D、(17,1)12. 已知函数f(x)=ax2+(a-1)lnx+1(a<u),设A,B为函数f(x)图象上的任意两点,若直线AB的斜率的绝对值不小于2,则实数a的取值范围是( )A、(-∞, ] B、[ ,0) C、(-∞, ] D、[ ,0)二、填空题:本大题共4小题,每小题5分,共20分。
-
13. 已知离散型随机变量X的分布列为
X
1
2
3
P
m
则m=
14. 已知(x-1)2=a0+a1x+a2x2+……+a7x7 , 则a1+a2+……+a7=15. 已知函数f(x)的定义域为R,f(-2)=-2,若对 x=R,f'(x)<3,则不等式f(x)>3x+4的解集为
16. 羽毛球比赛中,采用三局二胜制,已知任一局甲胜的概率为p,若甲赢得比赛的概率为g,则q-p取得最大值时p=
x=R,f'(x)<3,则不等式f(x)>3x+4的解集为
16. 羽毛球比赛中,采用三局二胜制,已知任一局甲胜的概率为p,若甲赢得比赛的概率为g,则q-p取得最大值时p=三、解答题:本大题共6小题,共70分.
-
17. 已知(x+ )n的展开式中前三项的系数成等差数列。(1)、求展开式的二项式系数的和;(2)、求展开式中含x2的项。18. 已知函数f(x)=9x-x2-lnx.(1)、求曲线f(x)在点(1,f(1))处的切线方程;(2)、设g(x)=f(x)+lnx,M(t,g(t))是曲线g(x)上的任意一点,过M作x轴的垂线,垂足为N,当x∈(0,9)时,求△OMN面积的最大值.19. 某厂生产A产品的产量x(件)与相应的耗电量y(度)的统计数据如下表所示:
x
2
3
4
5
6
y
2
3
5
7
8
经计算: , ≈16.12
附:相关系数r= , ,
(1)、计算(xi , yi)(i=1,2,3,4,5)的相关系数;(2)、求y关于x的线性回归方程 ,并预测生产10件产品所耗电的度数。20. 某地区为调查新生婴儿健康状况,随机抽取6名8个月龄婴儿称量体重(单位:千克),称量结果分别为6,8,9,9,9.5,10.已知8个月龄婴儿体重超过7.2千克,不超过9.8千克为“标准体重”,否则为“不标准体重”。(1)、根据样本估计总体思想,将频率视为概率,若从该地区全部8个月龄婴儿中任选3名进行称重,则至少有2名婴儿为“标准体重”的概率是多少?(2)、从抽取的6名婴儿中,随机选取4名,设x表示抽到的“标准体重”人数,求x的分布列和数学期望.21. 某市举办数学知识竞赛活动,共5000名学生参加,竞赛分为初试和复试,复试环节共3道题,其中1道多选题,2道单选题,得分规则如下:参赛学生每答对一道单选题得2分,答错得0分,答对多选题得3分,答错得0分,答完3道题后的得分之和为参赛学生的复试成绩.附:P(μ-σ<X<μ+σ)=0.6826,P(μ-2σ<X<μ+2σ)=0.9544,P(μ-3σ<K<μ+3σ)=0.9974.
(1)、通过分析可以认为学生初试成绩x服从正态分布N(u,o2),其中u=66,02=144,试估计初试成绩不低于90分的人数;(2)、已知小强已通过初试,他在复试中单选题的正答率为 ,多选题的正答率为 ,且每道题回答正确与否互不影响.记小强复试成绩为Y,求Y的分布列及数学期望。22. 已知函数f(x)=- x2-(a+1)x+alnx +a.(1)、讨论函数f(x)的单调性;(2)、判断函数f(x)能否有3个零点,若能,求出a的取值范围;若不能,请说明理由。