广西梧州市2019届数学中考一模试卷
试卷更新日期:2019-08-26 类型:中考模拟
一、单选题
-
1. ﹣5的相反数是( )A、5 B、﹣5 C、 D、-2. 不等式x﹣2>0在数轴上表示正确的是( )A、
 B、
B、 C、
C、 D、
D、 3. 有下列图形:①平行四边形;②有一个角是30°的直角三角形;③菱形;④等腰三角形,其中是轴对称图形的有( )A、4个 B、3个 C、2个 D、1个4. 在数轴上,点A表示的数是﹣4,点B表示的数是2,线段AB的中点表示的数为( )A、1 B、﹣1 C、3 D、﹣35. 下列根式中,与 是同类二次根式的是( )A、 B、 C、 D、6. 下列各图中,经过折叠能围成一个正方体的是( )A、
3. 有下列图形:①平行四边形;②有一个角是30°的直角三角形;③菱形;④等腰三角形,其中是轴对称图形的有( )A、4个 B、3个 C、2个 D、1个4. 在数轴上,点A表示的数是﹣4,点B表示的数是2,线段AB的中点表示的数为( )A、1 B、﹣1 C、3 D、﹣35. 下列根式中,与 是同类二次根式的是( )A、 B、 C、 D、6. 下列各图中,经过折叠能围成一个正方体的是( )A、 B、
B、 C、
C、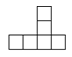 D、
D、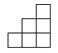 7. 已知关于x的一元二次方程2x2+mx﹣3=0的一个根是﹣1,则另一个根是( )A、1 B、﹣1 C、 D、8. 已知△ABC两条边的长分别为5和8,若第三边长为5的倍数,则第三边的长度是( )A、5 B、5或10 C、10或15 D、159. 以原点O为位似中心,作△ABC的位似图形△A'B'C',△ABC与△A'B'C'相似比为3,若点C的坐标为(4,1),则点C’的坐标为( )A、(12,3) B、(﹣12,3)或(12,﹣3) C、(﹣12,﹣3) D、(12,3)或(﹣12,﹣3)10. 如图,在△ABC中,∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,则CE长为( )
7. 已知关于x的一元二次方程2x2+mx﹣3=0的一个根是﹣1,则另一个根是( )A、1 B、﹣1 C、 D、8. 已知△ABC两条边的长分别为5和8,若第三边长为5的倍数,则第三边的长度是( )A、5 B、5或10 C、10或15 D、159. 以原点O为位似中心,作△ABC的位似图形△A'B'C',△ABC与△A'B'C'相似比为3,若点C的坐标为(4,1),则点C’的坐标为( )A、(12,3) B、(﹣12,3)或(12,﹣3) C、(﹣12,﹣3) D、(12,3)或(﹣12,﹣3)10. 如图,在△ABC中,∠B的平分线为BD,DE∥AB交BC于点E,若AB=9,BC=6,则CE长为( )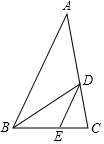 A、 B、 C、 D、11. 已知A(﹣1,y1),B(1,y2),C(2,y3)三点在抛物线y=x2﹣2x+m上,则y1、y2、y3的大小关系为( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y2<y3<y112. 已知⊙C的圆心的坐标是(4,0),半径为2,过点A(0,3)作⊙C的切线AB,点B为切点,则线段AB的长为( )A、5 B、4 C、 D、
A、 B、 C、 D、11. 已知A(﹣1,y1),B(1,y2),C(2,y3)三点在抛物线y=x2﹣2x+m上,则y1、y2、y3的大小关系为( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y2<y3<y112. 已知⊙C的圆心的坐标是(4,0),半径为2,过点A(0,3)作⊙C的切线AB,点B为切点,则线段AB的长为( )A、5 B、4 C、 D、二、填空题
-
13. 如图,直线a和直线b被直线c所截,若a∥b,∠1=40°,则∠2=.
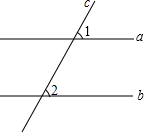 14. 计算(1﹣2a)﹣(2﹣2a)=.15. 分解因式:x3﹣xy2= .16. 某校规定学生的学期数学成绩满分为100分,其中平时成绩占30%,期末卷面成绩占70%.小李的平时成绩、期末卷面成绩(百分制)依次为90分、85分,则小李本学期的数学成绩是分.17. 在菱形ABCD中,AC=6,BD=8,则AB与CD之间的距离为.18. 如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC=.
14. 计算(1﹣2a)﹣(2﹣2a)=.15. 分解因式:x3﹣xy2= .16. 某校规定学生的学期数学成绩满分为100分,其中平时成绩占30%,期末卷面成绩占70%.小李的平时成绩、期末卷面成绩(百分制)依次为90分、85分,则小李本学期的数学成绩是分.17. 在菱形ABCD中,AC=6,BD=8,则AB与CD之间的距离为.18. 如图,四边形ABCD内接于⊙O,BC是⊙O的直径,AD∥BC,AC与BD相交于点P,若∠APB=50°,则∠PBC=.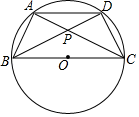
三、解答题
-
19. (﹣2)2+ ﹣4sin45°.20. 解方程组: .21. 2019年4月23日是“第二十四个世界读书日”,我市某中学发起了“读好书”活动.为了解九年级学生阅读“艺术类、科普类、文学类、军事类“这四类书籍的情况,数学老师随机抽查了该年级学生课外阅读的数量,绘制了下面不完整的条形图和扇形图.
 (1)、求本次抽查中阅读科普类书籍的人数,并补充完整条形图;(2)、小明要从这四类书籍中任选两类来阅读,请你用列表法或树状图求小明刚好选择科普类和军事类书籍的概率.22. 已知:点D是△ABC边BC上的中点,DE⊥AC,DF⊥AB,垂足分别是点E、F.
(1)、求本次抽查中阅读科普类书籍的人数,并补充完整条形图;(2)、小明要从这四类书籍中任选两类来阅读,请你用列表法或树状图求小明刚好选择科普类和军事类书籍的概率.22. 已知:点D是△ABC边BC上的中点,DE⊥AC,DF⊥AB,垂足分别是点E、F. (1)、若∠B=∠C,BF=CE,求证:△BFD≌△CED.(2)、若∠B+∠C=90°,求证:四边形AEDF是矩形.23. 随着无人机的应用范围日益广泛,无人机已走进寻常百姓家,如图,小明在我市体训基地试飞无人机.为测量无人机飞行的高度AB,小明在C点处测得∠ACB=45°,向前走5米,到达D点处测得∠ADB=40°.求无人机飞行的高度AB.(参考数据: ≈1.4,sin40°≈0.6,cos40°≈0.6,tan40°≈0.8.)
(1)、若∠B=∠C,BF=CE,求证:△BFD≌△CED.(2)、若∠B+∠C=90°,求证:四边形AEDF是矩形.23. 随着无人机的应用范围日益广泛,无人机已走进寻常百姓家,如图,小明在我市体训基地试飞无人机.为测量无人机飞行的高度AB,小明在C点处测得∠ACB=45°,向前走5米,到达D点处测得∠ADB=40°.求无人机飞行的高度AB.(参考数据: ≈1.4,sin40°≈0.6,cos40°≈0.6,tan40°≈0.8.) 24. 为响应习近平总书记提出的“绿水青山就是金山银山”的号召,今年植树节期间,学校组织七年级学生参加义务植树,美化校园活动.已知甲班共植树100棵,乙班共植树120棵,两班完成植树任务所用时间相同,且甲班每天比乙班少植树5棵.(1)、问甲、乙两班每天各植树多少棵?(2)、学校计划购进桂花树苗和榕树苗共200棵,桂花树苗每棵80元,榕树苗每棵70元.设桂花树苗买了x棵,购买两种树苗所需总费用为y元,求y与x的函数关系式.(3)、在(2)的条件下,如果购买榕树苗的数量不多于桂花树苗数量的一半,求购买桂花树苗多少棵时总费用最低?25. 如图,AC为∠BAM平分线,AB=10,以AB的长为直径作⊙O交AC于点D,过点D作DE⊥AM于点E.
24. 为响应习近平总书记提出的“绿水青山就是金山银山”的号召,今年植树节期间,学校组织七年级学生参加义务植树,美化校园活动.已知甲班共植树100棵,乙班共植树120棵,两班完成植树任务所用时间相同,且甲班每天比乙班少植树5棵.(1)、问甲、乙两班每天各植树多少棵?(2)、学校计划购进桂花树苗和榕树苗共200棵,桂花树苗每棵80元,榕树苗每棵70元.设桂花树苗买了x棵,购买两种树苗所需总费用为y元,求y与x的函数关系式.(3)、在(2)的条件下,如果购买榕树苗的数量不多于桂花树苗数量的一半,求购买桂花树苗多少棵时总费用最低?25. 如图,AC为∠BAM平分线,AB=10,以AB的长为直径作⊙O交AC于点D,过点D作DE⊥AM于点E.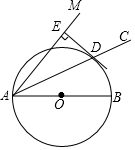 (1)、求证:DE是⊙O的切线.(2)、若DE=4,求AD的长.26. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a>0)与x轴交于点A(﹣2,0)和点B,与y轴交于点C,对称轴为直线x= .
(1)、求证:DE是⊙O的切线.(2)、若DE=4,求AD的长.26. 如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a>0)与x轴交于点A(﹣2,0)和点B,与y轴交于点C,对称轴为直线x= . (1)、请用a的代数式表示C点坐标.(2)、连接AC,BC,若△ABC的面积为10,求该抛物线的解析式.(3)、在(2)的条件下,点P是直线y=x+2上一点(位于x轴下方),点Q是反比例函数y= (k>0)图象上一点,若以点A,C,P,Q为顶点的四边形是菱形,则直接写出k的值(不需要写出计算过程).
(1)、请用a的代数式表示C点坐标.(2)、连接AC,BC,若△ABC的面积为10,求该抛物线的解析式.(3)、在(2)的条件下,点P是直线y=x+2上一点(位于x轴下方),点Q是反比例函数y= (k>0)图象上一点,若以点A,C,P,Q为顶点的四边形是菱形,则直接写出k的值(不需要写出计算过程).