广西柳州市鱼峰区十四中2019届数学中考模拟试卷
试卷更新日期:2019-08-26 类型:中考模拟
一、单选题
-
1. 已知室内温度为3℃,室外温度为﹣3℃,则室内温度比室外温度高( )A、6℃ B、﹣6℃ C、0℃ D、3℃2. 如图所示的几何体的俯视图是( ).
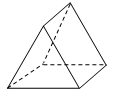 A、
A、 B、
B、 C、
C、 D、
D、 3. 下列图案中,可以看做是中心对称图形的有()
3. 下列图案中,可以看做是中心对称图形的有()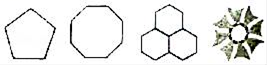 A、1个 B、2个 C、3个 D、4个4. 在一个不透明的口袋中装有5张完全相同的卡片,卡片上面分别写有数字-2、-1、0、1、3,从中随机抽出一张卡片,卡片上面的数字是负数的概率为( )A、0.8 B、0.6 C、0.4 D、0.25. 人类的遗传物质就是DNA,人类的DNA是很长的链,最短的22号染色体也长达30000000个核苷酸,30000000用科学记数法表示为( )A、3×108 B、3×107 C、3×106 D、0.3×1086. 如图,直线a∥b,直角三角形如图放置,∠DCB=90°.若∠1+∠B=70°,则∠2的度数为( )
A、1个 B、2个 C、3个 D、4个4. 在一个不透明的口袋中装有5张完全相同的卡片,卡片上面分别写有数字-2、-1、0、1、3,从中随机抽出一张卡片,卡片上面的数字是负数的概率为( )A、0.8 B、0.6 C、0.4 D、0.25. 人类的遗传物质就是DNA,人类的DNA是很长的链,最短的22号染色体也长达30000000个核苷酸,30000000用科学记数法表示为( )A、3×108 B、3×107 C、3×106 D、0.3×1086. 如图,直线a∥b,直角三角形如图放置,∠DCB=90°.若∠1+∠B=70°,则∠2的度数为( )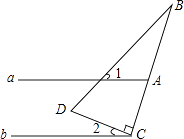 A、20° B、40° C、30° D、25°7. 如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC=130°,则∠D等于( )
A、20° B、40° C、30° D、25°7. 如图,AB是⊙O的直径,C,D为圆上两点,若∠AOC=130°,则∠D等于( ) A、20° B、25° C、35° D、50°8. 小华有x元,小林的钱数是小华的一半还多2元,小林的钱数是( )A、 B、 C、 D、9. 下列调查方式合适的是( )A、为了了解电视机的使用寿命,采用普查的方式 B、为了了解全国中学生的视力状况,采用普查的方式 C、对载人航天器“神舟十一号”零部件的检查,采用抽样调查的方式 D、为了了解人们保护水资源的意识,采用抽样调查的方式10. 下列各式中,能用平方差公式计算的是( )A、 B、 C、 D、11.
A、20° B、25° C、35° D、50°8. 小华有x元,小林的钱数是小华的一半还多2元,小林的钱数是( )A、 B、 C、 D、9. 下列调查方式合适的是( )A、为了了解电视机的使用寿命,采用普查的方式 B、为了了解全国中学生的视力状况,采用普查的方式 C、对载人航天器“神舟十一号”零部件的检查,采用抽样调查的方式 D、为了了解人们保护水资源的意识,采用抽样调查的方式10. 下列各式中,能用平方差公式计算的是( )A、 B、 C、 D、11.如图,正方形ABCD的边长为4,点P、Q分别是CD、AD的中点,动点E从点A向点B运动,到点B时停止运动;同时,动点F从点P出发,沿P→D→Q运动,点E、F的运动速度相同.设点E的运动路程为x,△AEF的面积为y,能大致刻画y与x的函数关系的图象是( )
 A、
A、 B、
B、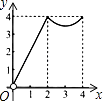 C、
C、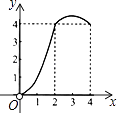 D、
D、
二、填空题
-
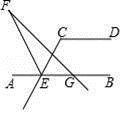
12. 如图,AB∥CD,∠DCE=118°,∠AEC的角平分线EF与GF相交于点F,∠BGF=132°,则∠F的度数是.
 13. 已知点P在第二象限,点P到x轴的距离是2,到y轴的距离是3,那么点P的坐标是14. 不等式4x﹣8<0的解集是.15. 已知方程x2+mx+3=0的一个根是1,则它的另一个根是 , m的值是。
13. 已知点P在第二象限,点P到x轴的距离是2,到y轴的距离是3,那么点P的坐标是14. 不等式4x﹣8<0的解集是.15. 已知方程x2+mx+3=0的一个根是1,则它的另一个根是 , m的值是。
16. 某公司向银行申请了甲、乙两种贷款,共计68万元,每年需付出8.42万元利息。已知甲种贷款每年的利率为12%,乙种贷款每年的利率为13%,则该公司甲、乙两种贷款的数额分别为.17. 如图,B、C、D依次为一直线上4个点,BC=3,△BCE为等边三角形,⊙O过A、D、E三点,且∠AOD=120°.设AB=x,CD=y,则y与x的函数关系式为.
三、解答题
-
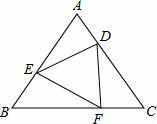
18. 计算: .19. 解分式方程:20. 如图,已知△ABC是正三角形,D,E,F分别是各边上的一点,且AD=BE=CF.请你说明△DEF是正三角形.
 21. 为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
21. 为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时.为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题: (1)、在这次调查中共调查了多少名学生?(2)、求户外活动时间为1.5小时的人数,并补充频数分布直方图;(3)、户外活动时间的众数和中位数分别是多少?(4)、若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?22. 如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.
(1)、在这次调查中共调查了多少名学生?(2)、求户外活动时间为1.5小时的人数,并补充频数分布直方图;(3)、户外活动时间的众数和中位数分别是多少?(4)、若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?22. 如图,在四边形ABCD中,BD为一条对角线,AD∥BC,AD=2BC,∠ABD=90°,E为AD的中点,连接BE.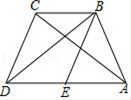 (1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,判断AC与CD的数量关系和位置关系,并说明理由.23. 已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,直线AB与y轴交于点C.
(1)、求证:四边形BCDE为菱形;(2)、连接AC,若AC平分∠BAD,判断AC与CD的数量关系和位置关系,并说明理由.23. 已知A(n,-2),B(1,4)是一次函数y=kx+b的图象和反比例函数y= 的图象的两个交点,直线AB与y轴交于点C.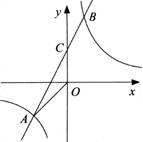 (1)、求反比例函数和一次函数的关系式;(2)、求△AOC的面积;(3)、求不等式kx+b- <0的解集(直接写出答案).24. 如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C.
(1)、求反比例函数和一次函数的关系式;(2)、求△AOC的面积;(3)、求不等式kx+b- <0的解集(直接写出答案).24. 如图,AB是⊙O的直径,弦DE垂直平分半径OB,垂足为M,DE=4,连接AD,过E作AD平行线交AB延长线于点C. (1)、求⊙O的半径;(2)、求证:CE是⊙O的切线;(3)、若弦DF与直径AB交于点N,当∠DNB=30°时,求图中阴影部分的面积.25. 如图1,已知抛物线L:y=ax2+bx﹣1.5(a>0)与x轴交于点A(-1,0)和点B,顶点为M,对称轴为直线l:x=1.
(1)、求⊙O的半径;(2)、求证:CE是⊙O的切线;(3)、若弦DF与直径AB交于点N,当∠DNB=30°时,求图中阴影部分的面积.25. 如图1,已知抛物线L:y=ax2+bx﹣1.5(a>0)与x轴交于点A(-1,0)和点B,顶点为M,对称轴为直线l:x=1. (1)、直接写出点B的坐标及一元二次方程ax2+bx﹣1.5=0的解.(2)、求抛物线L的解析式及顶点M的坐标.(3)、如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的頂点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m
(1)、直接写出点B的坐标及一元二次方程ax2+bx﹣1.5=0的解.(2)、求抛物线L的解析式及顶点M的坐标.(3)、如图2,设点P是抛物线L上的一个动点,将抛物线L平移.使它的頂点移至点P,得到新抛物线L′,L′与直线l相交于点N.设点P的横坐标为m①当m=5时,PM与PN有怎样的数量关系?请说明理由.
②当m为大于1的任意实数时,①中的关系式还成立吗?为什么?
③是否存在这样的点P,使△PMN为等边三角形?若存在.请求出点P的坐标;若不存在,请说明理由.