广西柳州市柳江区2019届数学中考模拟试卷（5月)

试卷更新日期：2019-08-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 在0，2，﹣2， $\frac{2}{3}$ 这四个数中，最大的数是（）

A、0 B、2 C、﹣2 D、 $\frac{2}{3}$

查看试题解析
2. 下列图形是轴对称图形的是（）

A、 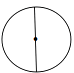B、 C、 D、

查看试题解析
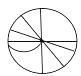3. 已知地球上海洋面积约为361 000 000km² ， 361 000 000这个数用科学记数法可表示为（）

A、3.61×10⁶ B、3.61×10⁷ C、3.61×10⁸ D、3.61×10⁹

查看试题解析
4. 下列计算的结果中正确的是（）

A、3x＋y=3xy B、5x²－2x²=3 C、2y²＋3y²=5y⁴ D、2xy³－2y³x=0

查看试题解析
5. 已知某几何体的三视图如图所示，那么这个几何体是（）

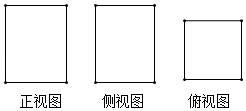A、长方体 B、圆柱 C、四棱锥 D、四棱台

查看试题解析
6. 从一副(54张)扑克牌中任意抽取一张，正好为K的概率为（）

A、 $\frac{2}{27}$ B、 $\frac{1}{4}$ C、 $\frac{1}{54}$ D、 $\frac{1}{2}$

查看试题解析
7. 在Rt△ABC中，∠C=90°，如果AC=2，cosA= $\frac{2}{3}$ ，那么AB的长是（）

A、3 B、 $\frac{4}{3}$ C、 $\sqrt{5}$ D、 $\sqrt{13}$

查看试题解析
8. 甲、乙两人进行射击比赛，在相同条件下各射击10次，他们的平均成绩一样，而他们的方差分别是S_甲²＝1.8，S_乙²＝0.7，则成绩比较稳定的是（）

A、甲稳定 B、乙稳定 C、一样稳定 D、无法比较

查看试题解析
9. 如图，将一张含有 $30^{\circ}$ 角的三角形纸片的两个顶点叠放在矩形的两条对边上，若 $∠ 2 = 44^{\circ}$ ，则 $∠ 1$ 的大小为（）

A、 $14^{\circ}$ B、 $16^{\circ}$ C、 $90^{\circ} - α$ D、 $α - 44^{\circ}$

查看试题解析
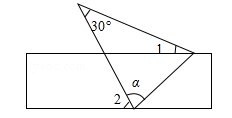10. 一件商品以进价120%的价格标价，后又打八折出售，最后这件商品是（）

A、赚了 B、亏了 C、不赚不亏 D、不确定盈亏

查看试题解析
11. 如图，AB是⊙O的直径，C是⊙O上一点（A，B除外），∠AOD＝136°，则∠C的度数是（）

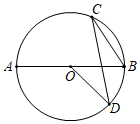A、44° B、22° C、46° D、36°

查看试题解析
12. 已知二次函数y=﹣x²+x+6及一次函数y=﹣x+m，将该二次函数在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，得到一个新函数（如图所示），请你在图中画出这个新图象，当直线y=﹣x+m与新图象有4个交点时，m的取值范围是（）

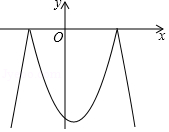A、﹣ $\frac{25}{4}$ ＜m＜3 B、﹣ $\frac{25}{4}$ ＜m＜2 C、﹣2＜m＜3 D、﹣6＜m＜﹣2

查看试题解析

二、填空题

13. 分解因式：a³﹣ab²= ．

查看试题解析
14. 如图，△ABC≌△DCB，∠DBC＝35°，则∠AOB的度数为.

查看试题解析
15. 如图，数轴上点A表示的数为 $a$ ，化简： $a + \sqrt{a^{2} - 4 a + 4}$ = ．

查看试题解析
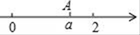16. 一个两位数，个位数字比十位数字大4，且个位数字与十位数字的和为10，则这个两位数为.

查看试题解析
17. 如图，以边长为1的正方形ABCD的边AB为对角线作第二个正方形AEBO₁ ，
再以BE为对角线作第三个正方形EFBO₂ ，如此作下去，…，则所作的第n个正方形的面积S_n＝.

查看试题解析

三、解答题

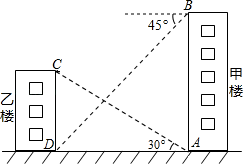
18. 解不等式组： ${\begin{array}{l} 1 + x > 0 \\ 2 x - 1 < 3 \end{array}$ .

查看试题解析
19. 解方程： $\frac{2}{x} + \frac{x}{x - 3} = 1$ .

查看试题解析
20. 如图，从甲楼底部A处测得乙楼顶部C处的仰角是30°，从甲楼顶部B处测得乙楼底部D处的俯角是45°，已知甲楼的高AB是100m，求乙楼的高CD（结果保留根号）.

查看试题解析
21. “每天锻炼一小时，健康生活一辈子”.为了选拔“阳光大课间”领操员，学校组织初中三个年级推选出来的15名领操员进行比赛，成绩如下表：

成绩/分

7

8

9

10

人数/人

2

5

4

4

(1)、这组数据的众数是多少，中位数是多少.

(2)、已知获得2018年四川省南充市的选手中，七、八、九年级分别有1人、2人、1人，学校准备从中随机抽取两人领操，求恰好抽到八年级两名领操员的概率.

查看试题解析
22. 如图，在四边形ABCD中，AC、BD相交于点O，且AO＝CO，AB∥CD.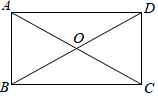

(1)、求证：AB＝CD；

(2)、若∠OAB＝∠OBA，求证：四边形ABCD是矩形.

查看试题解析
23. 如图，已知直线 $y = - x + 5$ 与双曲线 $y = \frac{6}{x}$ 交于A，B两点 $($ 点A在点B的上方 $)$ .

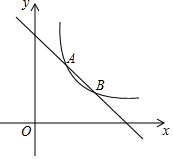(1)、求点A与点B的坐标；

(2)、点C在x轴上，若AC是等腰 $△ ABC$ 的腰，求符合条件的所有点C坐标.

查看试题解析
24. 一家商店销售某种商品，平均每天可售出20件，每件盈利40元为了扩大销售、增加盈利，该店采取了降价措施，在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件

(1)、若降价3元，则平均每天销售数量为多少件？

(2)、求每件商品降价多少元时，该商店每天销售利润为1200元？

(3)、求每件商品降价多少元时，该商店每天销售利润的最大值是多少元？

查看试题解析
25. 如图，△ABC内接于⊙O，∠CBG=∠A，CD为直径，OC与AB相交于点E，过点E作EF⊥BC，垂足为F，延长CD交GB的延长线于点P，连接BD.

(1)、求证：PG与⊙O相切；

(2)、若 $\frac{E F}{A C}$ = $\frac{5}{8}$ ，求 $\frac{B E}{O C}$ 的值；

(3)、在（2）的条件下，若⊙O的半径为8，PD=OD，求OE的长.

查看试题解析
26. 如图，直线l：y＝﹣3x+3与x轴、y轴分别相交于A、B两点，抛物线y＝ax²﹣2ax+a+4（a＜0）经过点B，交x轴正半轴于点C.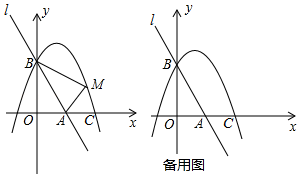

(1)、求该抛物线的函数表达式；

(2)、已知点M是抛物线上的一个动点，并且点M在第一象限内，连接AM、BM，设点M的横坐标为m，△ABM的面积为S，求S与m的函数表达式，并求出S的最大值及此时动点M的坐标；

(3)、将点A绕原点旋转得点A′，连接CA′、BA′，在旋转过程中，一动点M从点B出发，沿线段BA′以每秒3个单位的速度运动到A′，再沿线段A′C以每秒1个单位长度的速度运动到C后停止，求点M在整个运动过程中用时最少是多少？

查看试题解析

成绩/分	7	8	9	10
人数/人	2	5	4	4