广西柳州市2019届数学中考最后一卷

试卷更新日期：2019-08-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 2019年春节联欢晚会在某网站取得了同时在线人数超34100000的惊人成绩，创下了全球单平台网络直播记录，则34100000用科学记数法可表示为（）

A、 0.341×10⁸ B、3.41×10⁷ C、3.41×10⁸ D、34.1×10⁶

查看试题解析
2. 如图是由若干个大小相同的小正方体堆砌而成的几何体，那么其三种视图中周长最小的是（）

A、主视图 B、左视图 C、俯视图 D、三种一样

查看试题解析
3. 有的美术字是轴对称图形，下面四个美术字中可以看作轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 小明总结了以下结论：①a(b+c)＝ab+ac；②a(b﹣c)＝ab﹣ac；③(b﹣c)÷a＝b÷a﹣c÷a(a≠0)；④a÷(b+c)＝a÷b+a÷c(a≠0)；其中一定成立的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
5. 若反比例函数y＝ $\frac{2 - k}{x}$ 的图象位于第一、第三象限，则k的取值范围是（）

A、k＜2 B、k＞﹣2 C、k＜﹣2 D、k＞2

查看试题解析
6. 如图， $A B$ 是⊙ $O$ 的直径，点 $C$ ， $D$ 在⊙ $O$ 上.若 $∠ A B D = 55 °$ ，则 $∠ B C D$ 的度数为（）

A、 $25 °$ B、 $30 °$ C、 $35 °$ D、 $40 °$

查看试题解析
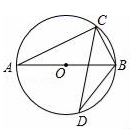7. 如图，O为平行四边形ABCD两对角线的交点，图中全等的三角形有（）

A、1对 B、2对 C、3对 D、4对

查看试题解析
8. 如果两组数据x₁ ， x₂、……x_n；y₁ ， y₂……y_n的平均数分别为 $\bar{x}$ 和 $\bar{y}$ ，那么新的一组数据2x₁+y₁ ， 2x₂+y₂……2x_n+y_n的平均数是（）

A、2 $\bar{x}$ B、2 $\bar{y}$ C、2 $\bar{x}$ + $\bar{y}$ D、 $\frac{4 \bar{x} + \bar{y}}{2}$

查看试题解析
9. 已知m是方程好x²－2x－1＝0的一个根，则代数式2m²－4m＋2019的值为（）

A、2022 B、2021 C、2020 D、2019

查看试题解析
10. 有甲、乙两个不同的水箱，容量分别为a升和b升，且已各装了一些水.若将甲中的水全倒入乙箱之后，乙箱还可以继续装20升水才会满；若将乙箱中的水倒入甲箱，装满甲箱后，乙箱里还剩10升水，则a，b之间的数量关系是（）

A、b＝a+15 B、b＝a+20 C、b＝a+30 D、b＝a+40

查看试题解析
11. “同吋掷两枚质地均匀的骰子，至少有一枚骰子的点数是3”的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{11}{36}$ C、 $\frac{5}{12}$ D、 $\frac{1}{4}$

查看试题解析
12. 我们规定：a*b= $\frac{a + b}{2}$ ，则下列等式中对于任意实数a、b、c都成立的是（   ）
①a+（b*c）=（a+b）*（a+c）     ②a*（b+c）=（a+b）*c
③a*（b+c）=（a*b）+（a*c）     ④（a*b）+c= $\frac{a}{2}$ +（b*2c）

A、①②③ B、①②④ C、①③④ D、②④

查看试题解析

二、填空题

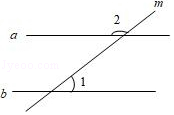
13. 已知多项式6x²+(1﹣2m)x+7m的值与m的取值无关，则x＝.

查看试题解析
14. 如图，直线a∥b，直线m与a，b均相交，若∠1＝38°，则∠2＝.

查看试题解析
15. 在一次摸球实验中，摸球箱内放有白色、黄色乒乓球共50个，这两种乒乓球的大小、材质都相同.小明发现，摸到白色乒乓球的频率稳定在60%左右，则箱内黄色乒乓球的个数很可能是.

查看试题解析
16. 如图，六边形ABCDEF是⊙O的内接正六边形，若正六边形的面积等于 $3 \sqrt{3}$ ，则⊙O的面积等于．

查看试题解析
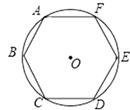17. Rt△ABC中，∠C＝90°，cosA＝ $\frac{3}{5}$ ，AC＝6cm，那么BC等于.

查看试题解析
18. 一组数据：1，2，x，y，4，6，其中x＜y，中位数是2.5，众数是2.则这组数据的平均数是；方差是。

查看试题解析

三、解答题

19. 计算（﹣ $\sqrt{2}$ ）²﹣|﹣3+5|+（1﹣ $\sqrt{3}$ ）⁰

查看试题解析
20. 如图，AP平分∠BAC，∠ADP和∠AEP互补.

(1)、作P到角两边AB，AC的垂线段PM，PN.

(2)、求证：PD＝PE.

查看试题解析

21. 材料1：

经济学家将家庭或个人在食品消费上的支出与总消费支出的比值称作恩格尔系数.即：恩格尔系数＝ $\frac{食品消费支出总额}{消费支出总额}$ ×100%.恩格尔系数可以用来刻划不同的消费结构，也能间接反映一个国家(地区)不同的发展阶段.联合国粮农组织的规定如表所示：

恩格尔系数

大于或等于60%

恩格尔系数

在50%～60%之间

恩格尔系数

在40%～50%之间

恩格尔系数

在30%～40%之间

恩格尔系数

小于30%

绝对贫困

温饱

小康

富裕

最富裕

(注：在50%﹣60%之间是指含50%，不含60%的所有数据，以此类推)

材料2：

2014年2月22日国家统计局上海调查总队报道：2013年上海市居民家庭生活消费总支出人均13425元.其中食品支出人均5334元(包括粮食支出450元，蔬菜及制品支出438元，肉禽蛋奶及制品支出1393元，水产品支出581元)，衣着支出人均771元，居住支出人均2260元，公用事业支出人均694元，交通通信支出人均1719元，文化教育支出人均964元，医疗保健支出人均1181元，其它支出人均502元.

根据上述材料，

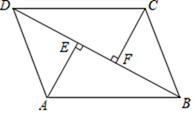
(1)、分别计算出“食品”、“衣着”、“居住”、“公用事业”、“交通通信”、“文化教育”和“医疗保健”占家庭生活消费总支出的百分比，并补充完成下列扇形统计图.(百分号前保留一位小数，圆心角精确到1°)

(2)、计算上海市居民的恩格尔系数，并判断2013年上海市居民的生活水平.

查看试题解析

22. 如图，在四边形ABCD中，AB∥CD，AE⊥BD，CF⊥BD，垂足分别是E、F，DE=BF，
求证：四边形ABCD是平行四边形.

查看试题解析
23. 开学初，小芳和小亮去学校商店购买学习用品，小芳用30元钱购买钢笔的数量是小亮用25元钱购买笔记本数量的2倍，已知每支钢笔的价格比每本笔记本的价格少2元

(1)、求每支钢笔和每本笔记本各是多少元；

(2)、学校运动会后，班主任再次购买上述价格的钢笔和笔记本共50件作为奖品，奖励给校运动会中表现突出的同学，总费用不超过200元.请问至少要买多少支钢笔？

查看试题解析
24. 已知点A(﹣1，4)在反比例函数y＝ $\frac{k}{x}$ 的图象上，B(﹣4，n)在正比例函数y＝ $\frac{1}{2}$ x的图象上

(1)、写出反比例函数y＝ $\frac{k}{x}$ 的解析式；

(2)、求出点B的坐标.

查看试题解析
25. 如图，在Rt△ABC中，∠ACB＝90°，∠BAC的平分线AO交BC于点O，以O为圆心，OC长为半径作⊙O，⊙O交AO所在的直线于D、E两点(点D在BC左侧).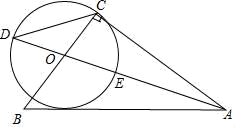

(1)、求证：AB是⊙O的切线；

(2)、连接CD，若AC＝ $\frac{2}{3}$ AD，求tan∠D的值；

(3)、在(2)的条件下，若⊙O的半径为5，求AB的长.

查看试题解析
26. 如图，已知抛物线y＝ax²+bx+5经过A(﹣5，0)，B(﹣4，﹣3)两点，与x轴的另一个交点为C，顶点为D，连结CD.

(1)、求该抛物线的表达式；

(2)、点P为该抛物线上一动点(与点B、C不重合)，设点P的横坐标为t.
①当点P在直线BC的下方运动时，求△PBC的面积的最大值；

②该抛物线上是否存在点P，使得∠PBC＝∠BCD？若存在，求出所有点P的坐标；若不存在，请说明理由.

查看试题解析