广西贺州市昭平县2019届数学中考一模试卷

试卷更新日期：2019-08-26 类型：中考模拟

进入出卷网下载

一、单选题

1. $- \frac{2}{3}$ 的绝对值是（）

A、 $- \frac{3}{2}$ B、 $- \frac{2}{3}$ C、 $\frac{2}{3}$ D、 $\frac{3}{2}$

查看试题解析
2. 某学校图书室藏书约15万册，用科学记数法表示15万这个数是（）

A、1.5×10³ B、1.5×10⁴ C、1.5×10⁵ D、1.5×10⁶

查看试题解析
3. 如图所示，AB∥CD，BC平分∠ABD，若∠C=40°，则∠D的度数为（）

A、90° B、100° C、110° D、120°

查看试题解析
4. 如图，晚上小亮在路灯下散步，在小亮由A处径直走到B处这一过程中，他在地上的影子（）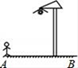

A、逐渐变短 B、先变短后变长 C、先变长后变短 D、逐渐变长

查看试题解析
5. 下列各因式分解正确的是（）

A、﹣x²+（﹣2）²＝（x+2）（x﹣2） B、x²+2x﹣1＝（x﹣1）² C、x³﹣4x＝x（x+2）（x﹣2） D、（2x﹣1）²＝4x²﹣4x+1

查看试题解析
6. 下列语句描述的事件中，是不可能事件的是（）

A、只手遮天，偷天换日 B、心想事成，万事如意 C、瓜熟蒂落，水到渠成 D、水能载舟，亦能覆舟

查看试题解析
7. 如图，已知点E在正方形ABCD内，满足∠AEB=90°，AE=6，BE=8，则阴影部分的面积是（）

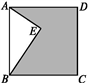A、48 B、60 C、76 D、80

查看试题解析
8. 下列选项中，阴影部分面积最小的是（）

A、 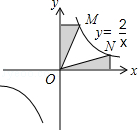B、 C、 D、

查看试题解析
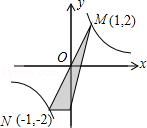9. 如图，CD是⊙O的直径，AB是弦（不是直径），AB⊥CD于点E，则下列结论正确的是（）

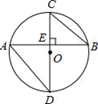A、AE＞BE B、 $\overset{⌢}{A D}$ ＝ $\overset{⌢}{B C}$ C、∠D＝ $\frac{1}{2}$ ∠AEC D、△ADE∽△CBE

查看试题解析
10. 二次函数y＝ax²+bx+c（a≠0）的图象的对称轴是直线x＝1，其图象的一部分如图所示.下列说法错误的是（）

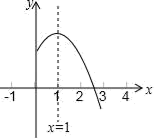A、abc＜0 B、a﹣b+c＜0 C、3a+c＜0 D、当﹣1＜x＜3时，y＞0

查看试题解析
11. 如图，有一直径是 $\sqrt{2}$ 米的圆形铁皮，现从中剪出一个圆周角是90°的最大扇形ABC，用该扇形铁皮围成一个圆锥，则所得圆锥的底面圆的半径为（）

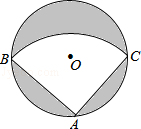A、 $\frac{\sqrt{2}}{2}$ 米 B、 $\frac{\sqrt{2}}{4}$ 米 C、 $\frac{1}{2}$ 米 D、 $\frac{1}{4}$ 米

查看试题解析
12. 若x是不等于1的实数，我们把 $\frac{1}{1 - x}$ 称为x的差倒数，如2的差倒数是 $\frac{1}{1 - x}$ ＝﹣1，﹣1的差倒数为 $\frac{1}{1 - (- 1)}$ ＝ $\frac{1}{2}$ ，现已知x₁＝ $\frac{1}{3}$ ，x₂是x₁的差倒数，x₃是x₂的差倒数，x₄是x₃的差倒数，…，依此类推，则x₂₀₁₉的值为（）

A、﹣ $\frac{1}{3}$ B、﹣2 C、3 D、4

查看试题解析

二、填空题

13. 若分式 $\frac{1}{2 x - 3}$ 有意义，则x的取值范围是．

查看试题解析
14. 方程组 ${\begin{matrix} \end{matrix} \begin{matrix} x + y = 3 \\ 2 x - y = 6 \end{matrix}$ 的解为.

查看试题解析
15. 一个数学学习兴趣小组有6名女生，4名男生，现要从这10名学生中选出1人担任组长，则男生当选组长的概率是.

查看试题解析
16. 定义：给定关于x的函数y，对于该函数图象上任意两点(x₁ ， y₁)，(x₂ ， y₂)，当x₁＜x₂时，都有y₁＜y₂ ，称该函数为增函数，根据以上定义，可以判断下面所给的函数中：①y＝2x；②y＝﹣x+1；③y＝x²(x＞0)；④y＝﹣ $\frac{1}{x}$ .是增函数的有(填上所有正确答案的序号)

查看试题解析
17. 如图，已知正方形ABCD的对角线长为3 $\sqrt{2}$ ，将正方形ABCD沿直线EF折叠，则图中阴影部分的周长为.

查看试题解析

三、解答题

18. 计算： $\sqrt{8}$ ﹣（2019﹣π）⁰﹣4cos45°+（﹣2）²

查看试题解析
19. 先化简，再求值： $\frac{x^{2}}{x^{2} + 4 x + 4} \div \frac{x}{x + 2} - \frac{x - 1}{x + 2}$ ，其中x= $\sqrt{2}$ ﹣1.

查看试题解析
20. 如图，点A，B，C，D在同一条直线上，点E，F分别在直线AD的两侧，且AE＝DF，∠A＝∠D，AB＝DC

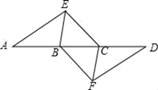(1)、求证：四边形BFCE是平行四边形；

(2)、如果AD＝5，DC＝ $\frac{3}{2}$ ，∠EBD＝60°，那么当四边形BFCE为菱形时BE的长是多少？

查看试题解析
21. 在“学习雷锋活动月”中，某校九（2）班全班同学都参加了“广告清除、助老助残、清理垃圾、义务植树”四个志愿活动（每人只参加一个活动）.为了了解情况，小明收集整理相关的数据后，绘制如图所示，不完整的统计图.请你根据统计图中所提供的信息解答下列问题：

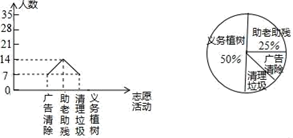(1)、求该班的人数；

(2)、请把折线统计图补充完整；

(3)、求扇形统计图中，广告清除部分对应的圆心角的度数.

查看试题解析
22. 周末，黄飞在广场放风筝.如图，为了计算风筝离地面的高度，黄飞测得风筝的仰角为60°，已知风筝线BC的长为15米，黄飞的身高AB为1.53米，请你帮小强画出测量示意图，并计算出风筝离地面的高度.（结果精确到1米，参考数据： $\sqrt{2}$ ≈1414， $\sqrt{3}$ ≈1.73）

查看试题解析
23. 某景点的门票价格如表

购票人数/人

1～40

41～80

80以上

每人门票价/元

10

8

6

某校九年级（1）、（2）两班计划去春游该景点，其中（1）班人数少于40人，（2）班人数多于40人且少于80人，如果两班都以班为单位单独购票，则一共支付838元：如果两班联合起来作为一个团体购票，则只需花费570元

(1)、两个班各有多少名学生；

(2)、团体购票与单独购票相比较，两个班各节约了多少钱？

查看试题解析
24. 如图，AB是⊙O的直径，AC是弦，直线EF经过点C，AD⊥EF于点D，∠DAC=∠BAC.

(1)、求证：EF是⊙O的切线；

(2)、求证：AC²=AD·AB；

(3)、若⊙O的半径为2，∠ACD=30⁰ ，求图中阴影部分的面积.

查看试题解析
25. 如图，在平面直角坐标系中，二次函数y＝﹣x²+bx+c的图象与x轴交于A、B两点，A点的坐标为（﹣3，0），B点在原点的左侧，与y轴交于点C（0，3），点P是直线BC上方的抛物线上一动点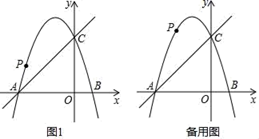

(1)、求这个二次函数的表达式；

(2)、连接PO、PC，并把△POC沿CO翻折，得到四边形POP′C（如图1所示），那么是否存在点P，使四边形POP′C为菱形？若存在，请此时点P的坐标：若不存在，请说明理由；

(3)、当点P运动到什么位置时，四边形ABCP的面积最大，并求出其最大值.

查看试题解析

购票人数/人	1～40	41～80	80以上
每人门票价/元	10	8	6