广西河池市两县一区2019届数学中考模拟试卷(一)
试卷更新日期:2019-08-26 类型:中考模拟
一、单选题
-
1. ﹣0.2的相反数是( )A、0.2 B、±0.2 C、﹣0.2 D、22. 已知一组数3、﹣2、1、﹣4、0,那么这组数的极差是( )A、3 B、4 C、6 D、73. 如图,直线a∥b,∠1=70°,那么∠2的度数是( )
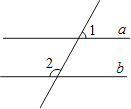 A、130° B、110° C、70° D、80°4. 如图,一个空间几何体的主视图和左视图都是正三角形,俯视图是一个圆,那么这个几何体是( )
A、130° B、110° C、70° D、80°4. 如图,一个空间几何体的主视图和左视图都是正三角形,俯视图是一个圆,那么这个几何体是( )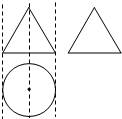 A、三角形 B、三棱柱 C、三棱锥 D、圆锥5. 若三角形的各边长分别是8cm、10cm和16cm,则以各边中点为顶点的三角形的周长为( )A、34cm B、30cm C、29cm D、17cm6. 在下列各组条件中,不能说明△ABC≌△DEF的是( )A、AB=DE,∠B=∠E,∠C=∠F B、AC=DF,BC=EF,∠A=∠D C、AB=DE,∠A=∠D,∠B=∠E D、AB=DE,BC=EF,AC=DF7. 如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )
A、三角形 B、三棱柱 C、三棱锥 D、圆锥5. 若三角形的各边长分别是8cm、10cm和16cm,则以各边中点为顶点的三角形的周长为( )A、34cm B、30cm C、29cm D、17cm6. 在下列各组条件中,不能说明△ABC≌△DEF的是( )A、AB=DE,∠B=∠E,∠C=∠F B、AC=DF,BC=EF,∠A=∠D C、AB=DE,∠A=∠D,∠B=∠E D、AB=DE,BC=EF,AC=DF7. 如图,在⊙O中,直径CD垂直于弦AB,若∠C=25°,则∠ABO的度数是( )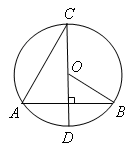 A、25° B、30° C、40° D、50°8. 下列事件中,是随机事件的是( )A、任意画一个三角形,其内角和为180° B、经过有交通信号的路口,遇到红灯 C、太阳从东方升起 D、任意一个五边形的外角和等于540°9. 下列关系式中,y不是自变量x的函数的是( )A、y=x B、y=x2 C、y=|x| D、y2=x10. 如图,将△ABC绕点C按逆时针方向旋转得△A′B′C,且A′点在AB上,A′B′交CB于点D,若∠BCB′=α,则∠CA′B′的度数为( )
A、25° B、30° C、40° D、50°8. 下列事件中,是随机事件的是( )A、任意画一个三角形,其内角和为180° B、经过有交通信号的路口,遇到红灯 C、太阳从东方升起 D、任意一个五边形的外角和等于540°9. 下列关系式中,y不是自变量x的函数的是( )A、y=x B、y=x2 C、y=|x| D、y2=x10. 如图,将△ABC绕点C按逆时针方向旋转得△A′B′C,且A′点在AB上,A′B′交CB于点D,若∠BCB′=α,则∠CA′B′的度数为( ) A、180°﹣α B、90° C、180° D、90°11. 如图,在扇形AOB中,∠AOB=90°,OA=2,点C、D分别为OA,OB的中点,分别以C。D为圆心,以OA。OB为直径作半圆,两半圆交于点E,则阴影部分的面积为( )
A、180°﹣α B、90° C、180° D、90°11. 如图,在扇形AOB中,∠AOB=90°,OA=2,点C、D分别为OA,OB的中点,分别以C。D为圆心,以OA。OB为直径作半圆,两半圆交于点E,则阴影部分的面积为( ) A、 B、 C、 D、12. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,D是AB边上一个动点(不与点A,B重合),E是BC边上一点,且∠CDE=30°.设AD=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
A、 B、 C、 D、12. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=2,D是AB边上一个动点(不与点A,B重合),E是BC边上一点,且∠CDE=30°.设AD=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、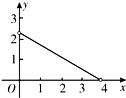 C、
C、 D、
D、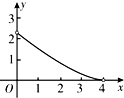
二、填空题
-
13. 若m+n=1,mn=2,则的值为 .14. 分解因式:9﹣12t+4t2=.15. 如图,有6张扑克牌,从中任意抽取两张,点数和是偶数的概率是.
 16. 一个直角三角形中,它的一个锐角的外角为135°,则这个三角形对称轴.(填“有”或“没有”)17. 计算;sin30°•tan30°+cos60°•tan60°= .18. 如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是.
16. 一个直角三角形中,它的一个锐角的外角为135°,则这个三角形对称轴.(填“有”或“没有”)17. 计算;sin30°•tan30°+cos60°•tan60°= .18. 如图,在△ABC中,AD是BC上的高,且BC=9,AD=3,矩形EFGH的顶点F、G在边BC上,顶点E、H分别在边AB和AC上,如果设边EF的长为x(0<x<3),矩形EFGH的面积为y,那么y关于x的函数解析式是.
三、解答题
-
19. 计算: .20. 化简: ,并从﹣1,0,1,2中选择一个合适的数求代数式的值.21. 如图,在图中求作⊙O,使⊙O满足以线段DE为弦,且圆心O到∠ABC两边的距离相等(要求:尺规作图,不写作法,保留作图痕迹)
 22. 某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分﹣74分;D级:60分以下)
22. 某校为了了解九年级学生体育测试成绩情况,以九年(1)班学生的体育测试成绩为样本,按A、B、C、D四个等级进行统计,并将统计结果绘制如下两幅统计图,请你结合图中所给信息解答下列问题:(说明:A级:90分﹣100分;B级:75分﹣89分;C级:60分﹣74分;D级:60分以下) (1)、写出D级学生的人数占全班总人数的百分比为 , C级学生所在的扇形圆心角的度数为;(2)、该班学生体育测试成绩的中位数落在等级内;(3)、若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?23. 如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离( ≈1.732,结果精确到0.1m).
(1)、写出D级学生的人数占全班总人数的百分比为 , C级学生所在的扇形圆心角的度数为;(2)、该班学生体育测试成绩的中位数落在等级内;(3)、若该校九年级学生共有500人,请你估计这次考试中A级和B级的学生共有多少人?23. 如图所示,小王在校园上的A处正面观测一座教学楼墙上的大型标牌,测得标牌下端D处的仰角为30°,然后他正对大楼方向前进5m到达B处,又测得该标牌上端C处的仰角为45°.若该楼高为16.65m,小王的眼睛离地面1.65m,大型标牌的上端与楼房的顶端平齐.求此标牌上端与下端之间的距离( ≈1.732,结果精确到0.1m). 24. 随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?25. 如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF,
24. 随着新能源汽车的发展,某公交公司将用新能源公交车淘汰某一条线路上“冒黑烟”较严重的燃油公交车,计划购买A型和B型新能源公交车共10辆,若购买A型公交车1辆,B型公交车2辆,共需300万元;若购买A型公交车2辆,B型公交车1辆,共需270万元,(1)、求购买A型和B型公交车每辆各需多少万元?(2)、预计在该条线路上A型和B型公交车每辆年均载客量分别为80万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1000万元,且确保这10辆公交车在该线路的年均载客量总和不少于900万人次,则该公司有哪几种购车方案?哪种购车方案总费用最少?最少总费用是多少?25. 如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF, (1)、求证:OD=OP;(2)、求证:FE是⊙O的切线.26. 如图,抛物线y=﹣ x2+bx+c经过点B(2 ,0)、C(0,2)两点,与x轴的另一个交点为A.
(1)、求证:OD=OP;(2)、求证:FE是⊙O的切线.26. 如图,抛物线y=﹣ x2+bx+c经过点B(2 ,0)、C(0,2)两点,与x轴的另一个交点为A. (1)、求抛物线的解析式;(2)、点D从点C出发沿线段CB以每秒 个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).
(1)、求抛物线的解析式;(2)、点D从点C出发沿线段CB以每秒 个单位长度的速度向点B运动,作DE⊥CB交y轴于点E,以CD、DE为边作矩形CDEF,设点D运动时间为t(s).①当点F落在抛物线上时,求t的值;
②若点D在运动过程中,设△ABC与矩形CDEF重叠部分的面积为S,请直接写出S与t之间的函数关系式,并写出自变量t的取值范围.