广西河池市2019届数学中考三模试卷
试卷更新日期:2019-08-26 类型:中考模拟
一、单选题
-
1. ﹣ 的倒数是( )A、7 B、﹣7 C、﹣ D、2. 单项式 的系数是( )A、 B、π C、2 D、3. 下列运算正确的是( )A、a2•a3=a6 B、(x2)3=x6 C、m6÷m2=m3 D、6a﹣4a=24. 若代数式 在实数范围内有意义,则实数x的取值范围是( )
A、x<3 B、x>3 C、x≠3 D、x=35. 如图,经过直线l外一点A作l的垂线,能画出( ) A、4条 B、3条 C、2条 D、1条6. 不等式组 的解集在数轴上表示为( )
A、4条 B、3条 C、2条 D、1条6. 不等式组 的解集在数轴上表示为( )
A、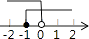 B、
B、 C、
C、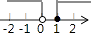 D、
D、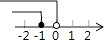 7. 以下是某校九年级10名同学参加学校演讲比赛的统计表:
7. 以下是某校九年级10名同学参加学校演讲比赛的统计表:成绩/分
80
85
90
95
人数/人
1
2
5
2
则这组数据的中位数和平均数分别为( )
A、90,90 B、90,89 C、85,89 D、85,908. 抛物线y=﹣(x﹣8)2+2的顶点坐标是( )A、(2,8) B、(8,2) C、(﹣8,2) D、(﹣8,﹣2)9. 下列几何体中,有一个几何体的主视图与俯视图的形状不一样,这个几何体是( )A、 正方体
B、
正方体
B、 圆柱
C、
圆柱
C、 圆锥
D、
圆锥
D、 球
10. 如图,⊙O是△ABC的外接圆,连接OA,OB,∠OBA=50°,则∠C的度数为( )
球
10. 如图,⊙O是△ABC的外接圆,连接OA,OB,∠OBA=50°,则∠C的度数为( ) A、30° B、40° C、50° D、80°11. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )
A、30° B、40° C、50° D、80°11. 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,ED⊥AB于D.如果∠A=30°,AE=6cm,那么CE等于( )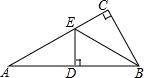 A、 cm B、2cm C、3cm D、4cm12. 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE、CD,PN、BF下列结论:①△ABE≌△DBC;②∠DFA=60°;③△BPN为等边三角形;④若∠1=∠2,则FB平分∠AFC.其中结论正确的有( )
A、 cm B、2cm C、3cm D、4cm12. 如图,点A,B,C在一条直线上,△ABD,△BCE均为等边三角形,连接AE、CD,PN、BF下列结论:①△ABE≌△DBC;②∠DFA=60°;③△BPN为等边三角形;④若∠1=∠2,则FB平分∠AFC.其中结论正确的有( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
13. 分解因式:ax2﹣ay2= .14. 计算: =.15. 某校抽查50名九年级学生对艾滋病三种主要传授途径的知晓情况,结果如表估计该校九年级600名学生中,三种传播途径都知道的有人.
传播途径(种)
0
1
2
3
知晓人数(人)
3
7
15
25
16. 在正方形网格中,∠AOB的位置如图所示,则cos∠AOB的值是. 17. 如图,底面圆半径是 的圆锥侧面展开图是一个圆心角为120°的扇形,则圆锥的母线l=.
17. 如图,底面圆半径是 的圆锥侧面展开图是一个圆心角为120°的扇形,则圆锥的母线l=. 18. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0)其部分图象如图所示,下列结论:①b2﹣4ac<0;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③2a+b=0,④当y>0时,x的取值范围是﹣1<x<3:⑤当x>0,y随x增大而减小,其中结论正确的序号是.
18. 如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0)其部分图象如图所示,下列结论:①b2﹣4ac<0;②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3; ③2a+b=0,④当y>0时,x的取值范围是﹣1<x<3:⑤当x>0,y随x增大而减小,其中结论正确的序号是.
三、解答题
-
19. 计算:2 (﹣3)﹣|﹣5|+(﹣1)2019+5tan45°.20. 先化简,再求值:(x+1)(x﹣1)﹣x(x﹣1),其中x= .21. 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).

①请画出△ABC向左平移5个单位长度后得到的△A B C ;
②请画出△ABC关于原点对称的△A B C ;
③在 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
22. 甲乙两名同学做摸球游戏,他们把三个分别标有1,2,3的大小和形状完全相同的小球放在一个不透明的口袋中.(1)、求从袋中随机摸出一球,标号是1的概率;(2)、从袋中随机摸出一球后放回,摇匀后再随机摸出一球,若两次摸出的球的标号之和为偶数时,则甲胜;若两次摸出的球的标号之和为奇数时,则乙胜;试分析这个游戏是否公平?请说明理由.23. 如图,AB⊥EF,DC⊥EF,垂足分别为B、C,且AB=CD,BE=CF.AF、DE相交于点O,AF、DC相交于点N,DE、AB相交于点M. (1)、请直接写出图中所有的等腰三角形;(2)、求证:△ABF≌△DCE.24. 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃.
(1)、请直接写出图中所有的等腰三角形;(2)、求证:△ABF≌△DCE.24. 制作一种产品,需先将材料加热达到60℃后,再进行操作.设该材料温度为y(℃),从加热开始计算的时间为x(分钟).据了解,设该材料加热时,温度y与时间x成一次函数关系;停止加热进行操作时,温度y与时间x成反比例关系(如图).已知该材料在操作加工前的温度为15℃,加热5分钟后温度达到60℃. (1)、分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;(2)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?(3)、该种材料温度维持在40℃以上(包括40℃)的时间有多长?25. 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.
(1)、分别求出将材料加热和停止加热进行操作时,y与x的函数关系式;(2)、根据工艺要求,当材料的温度低于15℃时,须停止操作,那么从开始加热到停止操作,共经历了多少时间?(3)、该种材料温度维持在40℃以上(包括40℃)的时间有多长?25. 如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C. (1)、求证:PE是⊙O的切线;
(1)、求证:PE是⊙O的切线;
(2)、求证:ED平分∠BEP;
(3)、若⊙O的半径为5,CF=2EF,求PD的长.
26. 如图1所示,已知抛物线 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上. (1)、直接写出D点和E点的坐标;(2)、点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时, =5:6?(3)、图2所示的抛物线是由 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
(1)、直接写出D点和E点的坐标;(2)、点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时, =5:6?(3)、图2所示的抛物线是由 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.