广西桂林市六校联考2019届第三次适应性考试数学试卷
试卷更新日期:2019-08-26 类型:中考模拟
一、单选题
-
1. 在1,0,﹣2,﹣1中,最大的数是( )A、1 B、0 C、﹣2 D、﹣12. 2018年政府工作报告指出,过去五年来,我国经济实力跃上新台阶.国内生产总值从54万亿元增加到82.7万亿元,稳居世界第二,82.7万亿用科学记数法表示为( )A、 0.827×1014 B、82.7×1012 C、8.27×1013 D、8.27×10143. 下列图形中,即是轴对称图形又是中心对称图形的是( )A、
 B、
B、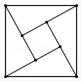 C、
C、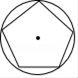 D、
D、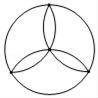 4. 已知直线l1∥l2 , 一块含30°角的直角三角板如图所示放置,∠1=35°,则∠2等于( )
4. 已知直线l1∥l2 , 一块含30°角的直角三角板如图所示放置,∠1=35°,则∠2等于( ) A、25° B、35° C、40° D、45°5. 已知点M(1﹣2m,m﹣1)在第一象限,则m的取值范围在数轴上表示正确的是( )A、
A、25° B、35° C、40° D、45°5. 已知点M(1﹣2m,m﹣1)在第一象限,则m的取值范围在数轴上表示正确的是( )A、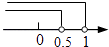 B、
B、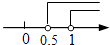 C、
C、 D、
D、 6. 用2、3、4三个数字排成一个三位数,则排出的数是偶数的概率为( )A、 B、 C、 D、7. 计算(﹣x5)7+(﹣x7)5的结果是( )A、﹣2x12 B、﹣2x35 C、﹣2x70 D、08. 一次函数y=﹣kx﹣k的图象可能是( )A、
6. 用2、3、4三个数字排成一个三位数,则排出的数是偶数的概率为( )A、 B、 C、 D、7. 计算(﹣x5)7+(﹣x7)5的结果是( )A、﹣2x12 B、﹣2x35 C、﹣2x70 D、08. 一次函数y=﹣kx﹣k的图象可能是( )A、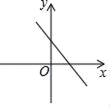 B、
B、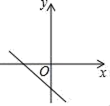 C、
C、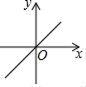 D、
D、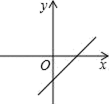 9. 使函数 有意义的自变量x的取值范围为( )A、x≠0 B、x≥﹣1 C、x≥﹣1且x≠0 D、x>﹣1且x≠010. 据统计,某省2015年的贫困人口约382万,截止2017年底,全省贫困人口约190万,设这两年全省贫困人口的年平均下降率为x,则下列方程正确的是( )A、382(1﹣2x)=190 B、382x2=190 C、382(1﹣x)2=190 D、382(1﹣x)+382(1﹣x)2=19011. 下列说法:①平方等于其本身的数有0,±1;②32xy3是4次单项式;③将方程 中的分母化为整数,得 =12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有( )A、1个 B、2个 C、3个 D、4个12. 在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则 的值是( ).
9. 使函数 有意义的自变量x的取值范围为( )A、x≠0 B、x≥﹣1 C、x≥﹣1且x≠0 D、x>﹣1且x≠010. 据统计,某省2015年的贫困人口约382万,截止2017年底,全省贫困人口约190万,设这两年全省贫困人口的年平均下降率为x,则下列方程正确的是( )A、382(1﹣2x)=190 B、382x2=190 C、382(1﹣x)2=190 D、382(1﹣x)+382(1﹣x)2=19011. 下列说法:①平方等于其本身的数有0,±1;②32xy3是4次单项式;③将方程 中的分母化为整数,得 =12;④平面内有4个点,过每两点画直线,可画6条、4条或1条.其中正确的有( )A、1个 B、2个 C、3个 D、4个12. 在数学拓展课《折叠矩形纸片》上,小林折叠矩形纸片ABCD进行如下操作:①把△ABF翻折,点B落在CD边上的点E处,折痕AF交BC边于点F;②把△ADH翻折,点D落在AE边长的点G处,折痕AH交CD边于点H.若AD=6,AB=10,则 的值是( ).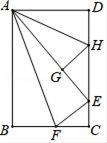 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 分解因式:x2﹣4x= .
14. 若分式 的值为零,则x的值为.
15. 一组数据6,3,9,4,3,5,11的中位数是.16. 若x+3=5﹣y,a,b互为倒数,则代数式 (x+y)+5ab=.17. 如图,正方形ABCD顶点C、D在反比例函数y= (x>0)图象上,顶点A、B分别在x轴、y轴的正半轴上,则点C的坐标为.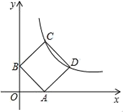 18. 如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C',其中点B的运动路径为 ,则图中阴影部分的面积为.
18. 如图,在△ABC中,∠ACB=90°,AC=BC=2,将△ABC绕AC的中点D逆时针旋转90°得到△A'B′C',其中点B的运动路径为 ,则图中阴影部分的面积为.
三、解答题
-
19. 计算:| -2|+2﹣1﹣cos60°﹣(1﹣ )0.20. 已知(x2+mx+1)(x2﹣2x+n)的展开式中不含x2和x3项.(1)、分别求m,n的值;(2)、先化简再求值:2n2+(2m+n)(m﹣n)﹣(m﹣n)221. 为了解本校九年级学生期末数学考试情况,小亮在九年级随机抽取了一部分学生的期末数学成绩为样本,分为A(100﹣90分)、B(89~80分)、C(79~60分)、D(59~0分)四个等级进行统计,并将统计结果绘制成如下统计图,请你根据统计图解答以下问题:
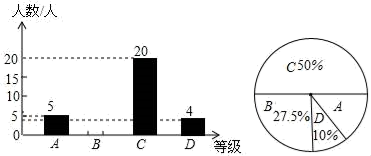 (1)、这次随机抽取的学生共有多少人?(2)、请补全条形统计图;(3)、这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?22. 某电器销售商到厂家选购A、B两种型号的液晶电视机,用30000元可购进A型电视10台,B型电视机15台;用30000元可购进A型电视机8台,B型电视机18台.(1)、求A、B两种型号的液晶电视机每台分别多少元?(2)、若该电器销售商销售一台A型液晶电视可获利800元,销售一台B型液晶电视可获利500元,该电器销售商准备用不超过40000元购进A、B两种型号液晶电视机共30台,且这两种液晶电视机全部售出后总获利不低于20400元,问:有几种购买方案?在这几种购买方案中,哪种方案获利最多?23. 如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1: 的斜坡CD前进2 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)、这次随机抽取的学生共有多少人?(2)、请补全条形统计图;(3)、这个学校九年级共有学生1200人,若分数为80分(含80分)以上为优秀,请估计这次九年级学生期末数学考试成绩为优秀的学生人数大约有多少?22. 某电器销售商到厂家选购A、B两种型号的液晶电视机,用30000元可购进A型电视10台,B型电视机15台;用30000元可购进A型电视机8台,B型电视机18台.(1)、求A、B两种型号的液晶电视机每台分别多少元?(2)、若该电器销售商销售一台A型液晶电视可获利800元,销售一台B型液晶电视可获利500元,该电器销售商准备用不超过40000元购进A、B两种型号液晶电视机共30台,且这两种液晶电视机全部售出后总获利不低于20400元,问:有几种购买方案?在这几种购买方案中,哪种方案获利最多?23. 如图,为测量学校旗杆AB的高度,小明从旗杆正前方6米处的点C出发,沿坡度为i=1: 的斜坡CD前进2 米到达点D,在点D处放置测角仪DE,测得旗杆顶部A的仰角为30°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直. (1)、求点D的铅垂高度(结果保留根号);(2)、求旗杆AB的高度(结果保留根号).24. 如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG
(1)、求点D的铅垂高度(结果保留根号);(2)、求旗杆AB的高度(结果保留根号).24. 如图1,已知AB是⊙O的直径,AC是⊙O的弦,过O点作OF⊥AB交⊙O于点D,交AC于点E,交BC的延长线于点F,点G是EF的中点,连接CG (1)、判断CG与⊙O的位置关系,并说明理由;(2)、求证:2OB2=BC•BF;(3)、如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.25. 如图,在平面直角坐标系中放置一直角三角板,其顶点为 , , ,将此三角板绕原点 顺时针旋转 ,得到 .
(1)、判断CG与⊙O的位置关系,并说明理由;(2)、求证:2OB2=BC•BF;(3)、如图2,当∠DCE=2∠F,CE=3,DG=2.5时,求DE的长.25. 如图,在平面直角坐标系中放置一直角三角板,其顶点为 , , ,将此三角板绕原点 顺时针旋转 ,得到 . (1)、如图,一抛物线经过点 ,求该抛物线解析式;(2)、设点 是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点 的坐标及面积的最大值.
(1)、如图,一抛物线经过点 ,求该抛物线解析式;(2)、设点 是在第一象限内抛物线上一动点,求使四边形 的面积达到最大时点 的坐标及面积的最大值.