广西贵港市2019届数学中考一模试卷
试卷更新日期:2019-08-26 类型:中考模拟
一、单选题
-
1. 的绝对值是( )A、 B、 C、 D、2. 新中国成立70年以来,中国铁路营业里程由52000公里增长到131000公里,将数据131000用科学记数法表示为( )A、13.1×105 B、13.1×104 C、1.31×106 D、1.31×1053. 如图所示的几何体的主视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列运算正确的是( )A、3a3+a3=4a6 B、(a+b)2=a2+b2 C、5a﹣3a=2a D、(﹣a)2•a3=﹣a65. 若一组数据9、6、x、7、5的平均数是2x,则这组数据的中位数是( )A、5 B、6 C、7 D、96. 某市决定从桂花、菊花、杜鹃花中随机选取一种作为市花,选到杜鹃花的概率是( )A、 B、 C、 D、17. 下列一元二次方程中,没有实数根的是( )A、2x2+3=0 B、x2=2x C、x2+4x﹣1=0 D、x2﹣8x+16=08. 下列命题中,是假命题的是( )A、任意多边形的外角和为360° B、在△ABC和△A′B′C′中,若AB=A′B′,BC=B′C′,∠C=∠C′=90°,则△ABC≌△A′B′C′ C、在一个三角形中,任意两边之差小于第三边 D、同弧所对的圆周角和圆心角相等9. 已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为( )A、﹣1 B、1 C、﹣3 D、310. 如图,直线a∥b,直线l与直线a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠2=40°,则∠1的度数为( )
4. 下列运算正确的是( )A、3a3+a3=4a6 B、(a+b)2=a2+b2 C、5a﹣3a=2a D、(﹣a)2•a3=﹣a65. 若一组数据9、6、x、7、5的平均数是2x,则这组数据的中位数是( )A、5 B、6 C、7 D、96. 某市决定从桂花、菊花、杜鹃花中随机选取一种作为市花,选到杜鹃花的概率是( )A、 B、 C、 D、17. 下列一元二次方程中,没有实数根的是( )A、2x2+3=0 B、x2=2x C、x2+4x﹣1=0 D、x2﹣8x+16=08. 下列命题中,是假命题的是( )A、任意多边形的外角和为360° B、在△ABC和△A′B′C′中,若AB=A′B′,BC=B′C′,∠C=∠C′=90°,则△ABC≌△A′B′C′ C、在一个三角形中,任意两边之差小于第三边 D、同弧所对的圆周角和圆心角相等9. 已知点P(1,a)与Q(b,2)关于x轴成轴对称,则a﹣b的值为( )A、﹣1 B、1 C、﹣3 D、310. 如图,直线a∥b,直线l与直线a、b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠2=40°,则∠1的度数为( ) A、20° B、30° C、40° D、50°11. 如图,在平面直角坐标系中,点P是以C(﹣ , )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是( )
A、20° B、30° C、40° D、50°11. 如图,在平面直角坐标系中,点P是以C(﹣ , )为圆心,1为半径的⊙C上的一个动点,已知A(﹣1,0),B(1,0),连接PA,PB,则PA2+PB2的最小值是( )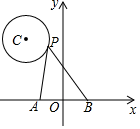 A、6 B、8 C、10 D、1212. 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B'作B'P∥BC,交AE于点P,连接BP.已知BC=3,CB'=1,下列结论:①AB=5;②sin∠ABP= ;③四边形BEB′P为菱形;④S四边形BEB'P﹣S△ECB'=1,其中正确的个数是( )
A、6 B、8 C、10 D、1212. 将矩形纸片ABCD折叠,使点B落在边CD上的B′处,折痕为AE,过B'作B'P∥BC,交AE于点P,连接BP.已知BC=3,CB'=1,下列结论:①AB=5;②sin∠ABP= ;③四边形BEB′P为菱形;④S四边形BEB'P﹣S△ECB'=1,其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
13. 9的算术平方根是 , = , ﹣ = .14. 将抛物线y=x2向下平移,若平移后的抛物线经过点A(2,1),则平移后的抛物线的解析式为.15. 不等式组 的最大整数解是.16. 如图,△DEF和△ABC是位似图形,点O是位似中心,点D,E,F分别时OA,OB,OC的中点,若△DEF的周长是2,则△ABC的周长是.
 17. 如图,在Rt△ABC中,∠ACB=90°,AC=2,∠A=60°,将△ABC绕BC的中点M顺时针旋转90°得到△DEF,其中点B的运动路径为弧BE,则图中阴影部分的面积为.
17. 如图,在Rt△ABC中,∠ACB=90°,AC=2,∠A=60°,将△ABC绕BC的中点M顺时针旋转90°得到△DEF,其中点B的运动路径为弧BE,则图中阴影部分的面积为. 18. 若a是不为2的有理数我们把 称为a的“哈利数”.如3的“哈利数”是 =﹣2;﹣2的“哈利数”是 ,已知a1=3,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,以此类推,a2019=.
18. 若a是不为2的有理数我们把 称为a的“哈利数”.如3的“哈利数”是 =﹣2;﹣2的“哈利数”是 ,已知a1=3,a2是a1的“哈利数”,a3是a2的“哈利数”,a4是a3的“哈利数”,以此类推,a2019=.三、解答题
-
19.(1)、计算:|1﹣ |+( )﹣1﹣2tan60°(2)、先化简,再求值: ,其中x= ﹣1.20. 尺规作图(只保留作图痕迹,不要求写出作法)
如图,已知∠a和线段a、b
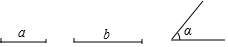
求作:
①△ABC,使∠A=∠α,AB=a,AC=b.
②在①的条件下,作AB边上的中线CD.
21. 关于x的一次函数y=ax+b与反比例函数y= (x>0)的图象交于点A(m,4)和点B(4,1).(1)、求m的值和反比例函数的解析式;(2)、求一次函数的解析式.22. 为了解某市市民上班时常用交通工具的状况,某课题小组随机调查了部分市民(问卷调查表如表所示),并根据调查结果绘制了如图所示的尚不完整的统计图:

根据以上统计图,解答下列问题:
(1)、本次接受调查的市民共有人;(2)、扇形统计图中,扇形B的圆心角度数是;(3)、请补全条形统计图;(4)、若该市“上班族”约有15万人,请估计乘公交车上班的人数.23. 为奖励表现优秀的学生,某校准备购买一批文具袋和圆规作为奖品,已知购买1个文具袋和2个圆规需21元;购买2个文具袋和3个圆规需39元.(1)、求文具袋和圆规的单价.(2)、学校准备购买文具袋20个,圆规若干.文具店给出两种优惠方案:方案一;购买一个文具袋送1个圆规.
方案二:购买圆规10个以上时,超出10个的部分按原价的八折优惠,文具袋不打折.若学校购买圆规100个,则选择哪种方案更合算?请说明理由.
24. 如图所示,△ABC中,点D是AB上一点,且AD=CD,以CD为直径的⊙O交BC于点E,交AC于点F,且点F是半圆CD的中点. (1)、求证:AB与⊙O相切.(2)、若tanB=2,AB=6,求CE的长度.25. 如图,直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c经过点A、B、C.
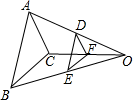
(1)、求证:AB与⊙O相切.(2)、若tanB=2,AB=6,求CE的长度.25. 如图,直线y=﹣x+c与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c经过点A、B、C. (1)、求点A的坐标和抛物线的解析式;(2)、当点P在抛物线上(不与点A重合),且△PBC的面积和△ABC的面积相等时,求出点P的横坐标.26. 如图1,在△ABC中,AB=AC,∠BAC=α,点D、E分别在边AB、AC上,AD=AE,连接DC,点F、P、G分别为DE、DC、BC的中点.
(1)、求点A的坐标和抛物线的解析式;(2)、当点P在抛物线上(不与点A重合),且△PBC的面积和△ABC的面积相等时,求出点P的横坐标.26. 如图1,在△ABC中,AB=AC,∠BAC=α,点D、E分别在边AB、AC上,AD=AE,连接DC,点F、P、G分别为DE、DC、BC的中点. (1)、观察猜想:图1中,线段PF与PG的数量关系是 , ∠FPG=(用含α的代数式表示)(2)、探究证明:当△ADE绕点A旋转到如图2所示的位置时,小新猜想(1)中的结论仍然成立,请你证明小新的猜想.(3)、拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=2,AB=6,请直接写出PF的最大值.
(1)、观察猜想:图1中,线段PF与PG的数量关系是 , ∠FPG=(用含α的代数式表示)(2)、探究证明:当△ADE绕点A旋转到如图2所示的位置时,小新猜想(1)中的结论仍然成立,请你证明小新的猜想.(3)、拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=2,AB=6,请直接写出PF的最大值.