广西百色市2019届数学考前最后一卷

试卷更新日期：2019-08-26 类型：中考模拟

进入出卷网下载

一、单选题

1. 已知△ABC中，∠A＝30°，则下列结论正确的是（）

A、0°＜∠B＜60° B、90°＜∠B＜150 C、0°＜∠B＜60°或90°＜∠B＜150° D、以上都不对

查看试题解析
2. 如图，直线a∥b，直角三角形如图放置，∠DCB＝90°，若∠1+∠B＝65°，则∠2的度数为（）

A、20° B、25° C、30° D、35°

查看试题解析
3. 一组数据按从小到大排列为2，4，8，x，10，14.若这组数据的中位数为9，则x是（）

A、6 B、8 C、9 D、10

查看试题解析
4. 方程 $\frac{2 - x}{x - 5} - \frac{3}{5 - x}$ ＝0的解为（）

A、﹣2 B、2 C、5 D、无解

查看试题解析
5. 如图的立体图形，从左面看可能是（）

A、 B、 C、 D、

查看试题解析
6. 已知地球上海洋面积约为316000000km² ，数据316 0 00 000用科学记数法可表示为（）

A、3.16×10⁹ B、3.16×10⁷ C、3.16×10⁸ D、3.16×10⁶

查看试题解析
7. 下列“数字图形”中，既是轴对称图形，又是中心对称图形的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 若不等式组 ${\begin{array}{l} x - 2 > 1 - 2 x \\ x + m \leq 0 \end{array}$ 有解，则 $m$ 的取值范围是（）

A、 $m > - 1$ B、 $m \geq - 1$ C、 $m \leq - 1$ D、 $m < - 1$

查看试题解析
9. 将抛物线y＝x²﹣2x﹣3沿x轴折得到的新抛物线的解析式为（）

A、y＝﹣x²+2x+3 B、y＝﹣x²﹣2x﹣3 C、y＝x²+2x﹣3 D、y＝x²﹣2x+3

查看试题解析
10. 如图是小刚进入中考复习阶段以来参加的10次物理水平测试成绩(满分70分)的统计图，那么关于这10次测试成绩，下列说法错误的是（）

A、中位数是55 B、众数是60 C、方差是26 D、平均数是54

查看试题解析
11. 下列命题的逆命题是真命题的是（）

A、如果两个角是直角，那么它们相等 B、全等三角形的对应角相等 C、两直线平行，内错角相等 D、对顶角相等

查看试题解析
12. 已知点A（a﹣2，2a+7），点B的坐标为（1，5），直线AB∥y轴，则a的值是（）

A、1 B、3 C、﹣1 D、5

查看试题解析

二、填空题

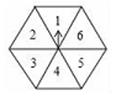
13. 如果数a与2互为相反数，那么a=.

查看试题解析
14. 若m，n为实数，且m＝ $\frac{\sqrt{1 - n} + \sqrt{n - 1}}{2 n}$ +8，则m+n的算术平方根为.

查看试题解析
15. 如图，任意转动正六边形转盘一次，当转盘停止转动时，指针指向大于3的数的概率是．

查看试题解析
16. 观察下列各等式：
$- 2 + 3 = 1$

$- 5 - 6 + 7 + 8 = 4$

$- 10 - 11 - 12 + 13 + 14 + 15 = 9$

$- 17 - 18 - 19 - 20 + 21 + 22 + 23 + 24 = 16$

……

根据以上规律可知第11行左起第一个数是.

查看试题解析
17. 在平面直角坐标系中，△ABC的一个顶点是A（2，3），若以原点O为位似中心，画三角形ABC的位似图形△A′B′C′，使△ABC与△A′B′C′的相似比为 $\frac{2}{3}$ ，则A′的坐标为.

查看试题解析
18. 我们知道：四边形具有不稳定性.如图，在平面直角坐标系xOy中，矩形ABCD的边AB在x轴上， $A (- 3 ， 0)$ ， $B (4 ， 0)$ ，边AD长为5.现固定边AB，“推”矩形使点D落在y轴的正半轴上（落点记为 $D^{'}$ ），相应地，点C的对应点 $C^{'}$ 的坐标为.

查看试题解析

三、解答题

19. 计算：﹣2⁴﹣ $\sqrt{12}$ +|1﹣4sin60°|+（2015π）⁰.

查看试题解析
20. 先化简，再求值（1﹣ $\frac{3}{x + 1}$ ）÷ $\frac{x^{2} - 4 x + 4}{x^{2} - 1}$ ，其中x＝4．

查看试题解析
21. 如图， $▱ A B C D$ 中，顶点 $A$ 的坐标是 $(0 ， 2)$ ， $A D ∥ x$ 轴， $B C$ 交 $y$ 轴于点 $E$ ，顶点 $C$ 的纵坐标是-4， $▱ A B C D$ 的面积是24．反比例函数 $y = \frac{k}{x}$ 的图象经过点 $B$ 和 $D$ ，求：

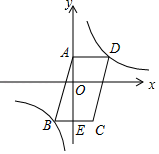(1)、反比例函数的表达式；

(2)、 $A B$ 所在直线的函数表达式．

查看试题解析
22. 在菱形ABCD中，点P是BC边上一点，连接AP，点E，F是AP上的两点，连接DE，BF，使得∠AED＝∠ABC，∠ABF＝∠BPF.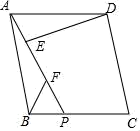

求证：

(1)、△ABF≌△DAE；

(2)、DE＝BF+EF.

查看试题解析

23. 为了解某校中学生对《最强大脑》、《朗读者》、《中国诗词大会》、《出彩中国人》四个电视节目的喜爱情况，随机抽取了x名学生进行调查统计（要求每名学生选出并且只能选出一个自己最喜爱的节目），并将调查结果绘制成如图统计图表：根据以上提供的信息，解答下列问题：

节目	人数（名）	百分比
最强大脑	5	10%
朗读者	15	b%
中国诗词大会	a	40%
出彩中国人	10	20%

(1)、x= ， a= ， b=；

(2)、补全上面的条形统计图；

(3)、在喜爱《最强大脑》的学生中，有2名女同学，其余为男同学，现要从中随机抽取2名同学代表学校参加潍坊市组织的竞赛活动，请用树状图或列表法求出所抽取的2名同学恰好是1名男同学和1名女同学的概率.

查看试题解析

24. 某书店购进甲、乙两种图书共100本，甲、乙两种图书的进价分别为每本15元、35元，甲、乙两种图书的售价分别为每本20元、45元.

(1)、若书店购书恰好用了2300元，求购进的甲、乙图书各多少本？

(2)、销售时，甲图书打8.5折，乙图书不打折.若甲、乙两种图书全部销售完后共获利 $\frac{1}{5}$ ，求购进的甲、乙图书各多少本？

查看试题解析
25. 如图，CD是⊙O的直径，点A为圆上一点不与C，D点重合，过点A作⊙O的切线，与DC的延长线交于点P，点M为AP上一点，连接MC并延长，与⊙O交于点F，E为CF上一点，且MA＝ME，连接AE并延长，与⊙O于点B，连接BC，AC.

(1)、求证： $\overset{⌢}{B C}$ ＝ $\overset{⌢}{B F}$ ；

(2)、若PC•PD＝7，求AP的长.

查看试题解析
26. 如图，已知抛物线的顶点为A(1，4)，抛物线与y轴交于点B(0，3)，与x轴交于C，D两点.点P是x轴上的一个动点.

(1)、求此抛物线的解析式；

(2)、当PA+PB的值最小时，求点P的坐标；

(3)、抛物线上是否存在一点Q(Q与B不重合)，使△CDQ的面积等于△BCD的面积？若存在，直接写出点Q的坐标；若不存在，请说明理由.

查看试题解析