初中数学浙教版九年级上册第一章 二次函数 单元检测
试卷更新日期:2019-08-22 类型:单元试卷
一、单选题
-
1. 某工厂2015年产品的产量为100吨,该产品产量的年平均增长率为x(x>0),设2017年该产品的产量为y吨,则y关于x的函数关系式为( )A、y=100(1﹣x)2 B、y=100(1+x)2 C、y= D、y=100+100(1+x)+100(1+x)22. 函数y=(m+2) +2x+1是二次函数,则m的值为( )A、﹣2 B、0 C、﹣2或1 D、13. 二次函数y=3x2﹣2x﹣4的二次项系数与常数项的和是( )A、1 B、﹣1 C、7 D、﹣64. 如图,边长都为4的正方形ABCD和正三角形EFG如图放置,AB与EF在一条直线上,点A与点F重合.现将△EFG沿AB方向以每秒1个单位的速度匀速运动,当点F与B重合时停止.在这个运动过程中,正方形ABCD和△EFG重叠部分的面积S与运动时间t的函数图象大致是( )
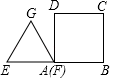 A、
A、 B、
B、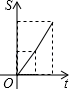 C、
C、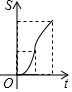 D、
D、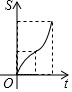 5. 从地面竖直向上抛出一小球,小球的高度 (单位: )与小球运动时间 (单位: )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度 时, .其中正确的是( )
5. 从地面竖直向上抛出一小球,小球的高度 (单位: )与小球运动时间 (单位: )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 ;②小球抛出3秒后,速度越来越快;③小球抛出3秒时速度为0;④小球的高度 时, .其中正确的是( ) A、①④ B、①② C、②③④ D、②③6. 设b>0,二次函数y=ax2+bx+a2﹣1的图象为下列之一,则a的值为( )
A、①④ B、①② C、②③④ D、②③6. 设b>0,二次函数y=ax2+bx+a2﹣1的图象为下列之一,则a的值为( )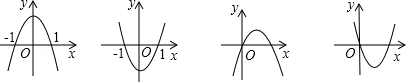 A、1 B、﹣1 C、 D、7. 如图,已知二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于C点,OA=OC,则由抛物线的特征写出如下结论:
A、1 B、﹣1 C、 D、7. 如图,已知二次函数y=ax2+bx+c的图象与x轴分别交于A、B两点,与y轴交于C点,OA=OC,则由抛物线的特征写出如下结论:
①abc>0;②4ac-b2>0;③a-b+c>0;④ac+b+1=0.
其中正确的个数是( )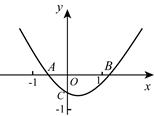 A、4个 B、3个 C、2个 D、1个8. 如图是函数 的图象,直线 轴且过点 ,将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( )
A、4个 B、3个 C、2个 D、1个8. 如图是函数 的图象,直线 轴且过点 ,将该函数在直线l上方的图象沿直线l向下翻折,在直线1下方的图象保持不变,得到一个新图象.若新图象对应的函数的最大值与最小值之差不大于5,则m的取值范围是( ) A、 B、 C、 D、 或9. 二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表,该抛物线的对称轴是直线( )
A、 B、 C、 D、 或9. 二次函数y=ax2+bx+c(a、b、c为常数且a≠0)中的x与y的部分对应值如下表,该抛物线的对称轴是直线( )x
﹣1
0
1
3
y
﹣1
3
5
3
A、x=0 B、x=1 C、x=1.5 D、x=210. 两位同学在足球场上玩游戏,两人的运动路线如图1所示,其中AC=DB,小王从点A出发沿线 段AB运动到点B,小林从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示,结合图象分析以下结论: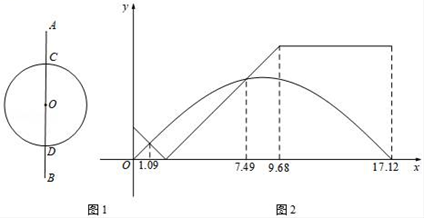
①小王的运动路程比小林的长②两人分别在1.09秒和7.49秒的时刻相遇③当小王运动到点D的时候,小林已经过了点D④在4.84秒时,两人的距离正好等于⊙O的半径上述说法正确的个数的是( )
A、 1个 B、 2个 C、 3个 D、 4个二、填空题
-
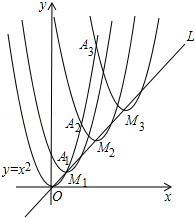
11. 已知抛物线y=ax2+bx+c(a≠0)经过点A(1,2)和B(-1,-6)两点,则a+c的值是12. 将二次函数 化成 的形式为.13. 如图,抛物线y=x2在第一象限内经过的整数点(横坐标,纵坐标都为整数的点)依次为A1 , A2 , A3 , …An , ….将抛物线y=x2沿直线L:y=x向上平移,得一系列抛物线,且满足下列条件:
①抛物线的顶点M1 , M2 , M3 , …Mn , …都在直线L:y=x上;
②抛物线依次经过点A1 , A2 , A3…An , ….
则M2016顶点的坐标为 .
 14. 若点M(﹣2,y1),N(﹣1,y2),P(8,y3)在抛物线y=﹣ x2 +2x上,则y1 , y2 , y3由小到大的顺序为 .15. 若点(﹣2,a),(﹣3,b)都在二次函数y=x2+2x+m的图象上,比较a、b的大小:ab.(填“>”“<”或“=”).16. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用 长的篱笆围成一个矩形花园 (篱笆只围 、 两边).设 ,若在 处有一棵树与墙 、 的距离分别是 和 ,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积 的最大值为 .
14. 若点M(﹣2,y1),N(﹣1,y2),P(8,y3)在抛物线y=﹣ x2 +2x上,则y1 , y2 , y3由小到大的顺序为 .15. 若点(﹣2,a),(﹣3,b)都在二次函数y=x2+2x+m的图象上,比较a、b的大小:ab.(填“>”“<”或“=”).16. 在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用 长的篱笆围成一个矩形花园 (篱笆只围 、 两边).设 ,若在 处有一棵树与墙 、 的距离分别是 和 ,要将这棵树围在花园内(含边界,不考虑树的粗细),则花园面积 的最大值为 .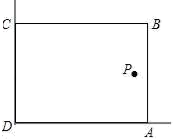
三、解答题
-
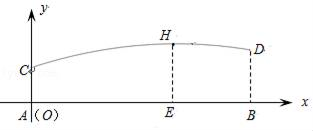
17. 已知抛物线的顶点为(1,﹣4),且过点(﹣2,5).(1)、求抛物线解析式;(2)、直接写出当函数值y>0时,自变量x的取值范围.18. 已知二次函数y=x2﹣2mx+1.记当x=c时,函数值为yc , 那么,是否存在实数m,使得对于满足0≤x≤1的任意实数a,b,总有ya+yb≥1.19. 甲、乙两人分别站在相距6米的A、B两点练习打羽毛球,已知羽毛球飞行的路线为抛物线的一部分,甲在离地面1米的C处发出一球,乙在离地面1.5米的D处成功击球,球飞行过程中的最高点H与甲的水平距离AE为4米,现以A为原点,直线AB为x轴,建立平面直角坐标系(如图所示).求羽毛球飞行的路线所在的抛物线的表达式及飞行的最高高度.
 20. 已知二次函数y=﹣x2+2x+3图象的对称轴为直线.
20. 已知二次函数y=﹣x2+2x+3图象的对称轴为直线. (1)、请求出该函数图象的对称轴;(2)、在坐标系内作出该函数的图象;(3)、有一条直线过点P(1,5),若该直线与二次函数y=﹣x2+2x+3只有一个交点,请求出所有满足条件的直线的关系式.21. 为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).
(1)、请求出该函数图象的对称轴;(2)、在坐标系内作出该函数的图象;(3)、有一条直线过点P(1,5),若该直线与二次函数y=﹣x2+2x+3只有一个交点,请求出所有满足条件的直线的关系式.21. 为响应荆州市“创建全国文明城市”号召,某单位不断美化环境,拟在一块矩形空地上修建绿色植物园,其中一边靠墙,可利用的墙长不超过18m,另外三边由36m长的栅栏围成.设矩形ABCD空地中,垂直于墙的边AB=xm,面积为ym2(如图).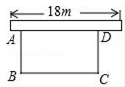 (1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若矩形空地的面积为160m2 , 求x的值;(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.
(1)、求y与x之间的函数关系式,并写出自变量x的取值范围;(2)、若矩形空地的面积为160m2 , 求x的值;(3)、若该单位用8600元购买了甲、乙、丙三种绿色植物共400棵(每种植物的单价和每棵栽种的合理用地面积如下表).问丙种植物最多可以购买多少棵?此时,这批植物可以全部栽种到这块空地上吗?请说明理由.甲
乙
丙
单价(元/棵)
14
16
28
合理用地(m2/棵)
0.4
1
0.4
22. “互联网+”时代,网上购物备受消费者青睐.某网店专售一款休闲裤,其成本为每条40元,当售价为每条80元时,每月可销售100条.为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售5条.设每条裤子的售价为x元(x为正整数),每月的销售量为y条.(1)、直接写出y与x的函数关系式;(2)、设该网店每月获得的利润为w元,当销售单价降低多少元时,每月获得的利润最大,最大利润是多少?(3)、该网店店主热心公益事业,决定每月从利润中捐出200元资助贫困学生.为了保证捐款后每月利润不低于4220元,且让消费者得到最大的实惠,该如何确定休闲裤的销售单价?23. 如图,已知抛物线y=-x2+bx+c与x轴交于A、B两点,AB=4,交y轴于点C,对称轴是直线x=1. (1)、求抛物线的解析式及点C的坐标;(2)、连接BC,E是线段OC上一点,E关于直线x=1的对称点F正好落在BC上,求点F的坐标;(3)、动点M从点O出发,以每秒2个单位长度的速度向点B运动,过M作x轴的垂线交抛物线于点N,交线段BC于点Q.设运动时间为t(t>0)秒.
(1)、求抛物线的解析式及点C的坐标;(2)、连接BC,E是线段OC上一点,E关于直线x=1的对称点F正好落在BC上,求点F的坐标;(3)、动点M从点O出发,以每秒2个单位长度的速度向点B运动,过M作x轴的垂线交抛物线于点N,交线段BC于点Q.设运动时间为t(t>0)秒.①若△AOC与△BMN相似,请直接写出t的值;
②△BOQ能否为等腰三角形?若能,求出t的值;若不能,请说明理由.
24. 如图,抛物线y= x2+bx+c的顶点为M,对称轴是直线x=1,与x轴的交点为A(-3,0)和B.将抛物线y= x2+bx+c绕点B逆时针方向旋转90°,点M1 , A1为点M,A旋转后的对应点,旋转后的抛物线与y轴相交于C,D两点.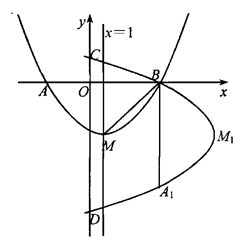 (1)、写出点B的坐标及求原抛物线的解析式:(2)、求证A,M,A1三点在同一直线上:(3)、设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大.如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.
(1)、写出点B的坐标及求原抛物线的解析式:(2)、求证A,M,A1三点在同一直线上:(3)、设点P是旋转后抛物线上DM1之间的一动点,是否存在一点P,使四边形PM1MD的面积最大.如果存在,请求出点P的坐标及四边形PM1MD的面积;如果不存在,请说明理由.