初中数学浙教版九年级上册1.4 二次函数的应用 基础巩固训练
试卷更新日期:2019-08-22 类型:同步测试
一、几何问题
-
1. 某农场拟建两间矩形饲养室,一面靠足够长的墙体,中间用一道围栏隔开,并在如图8所示的三处各留1m宽的门,所有围栏的总长(不含门)为27m,则能建成的饲养室面积最大为( )
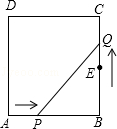
 A、75m2 B、 m2 C、48m2 D、 m22. 如图,AB=5,P是线段AB上的动点,分别以AP、BP为边,在线段AB的同侧作正方形APCD和正方形BPEF,连接CF,则CF的最小值是 .
A、75m2 B、 m2 C、48m2 D、 m22. 如图,AB=5,P是线段AB上的动点,分别以AP、BP为边,在线段AB的同侧作正方形APCD和正方形BPEF,连接CF,则CF的最小值是 . 3. 如图1是一块长为60cm的正方体薄铁片制作的一个长方体盒子,如果要做一个没有盖的长方体盒子,可先在薄铁片的四个角上截去四个相同的小正方形(如图2),然后把四边折合起来.
3. 如图1是一块长为60cm的正方体薄铁片制作的一个长方体盒子,如果要做一个没有盖的长方体盒子,可先在薄铁片的四个角上截去四个相同的小正方形(如图2),然后把四边折合起来.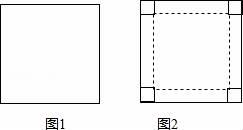 (1)、求做成的盒子底面积y(cm2)与截去小正方形边长x(cm2)之间的函数关系式;(2)、当做成的盒子的底面积为900cm2时,试求该盒子的容积.
(1)、求做成的盒子底面积y(cm2)与截去小正方形边长x(cm2)之间的函数关系式;(2)、当做成的盒子的底面积为900cm2时,试求该盒子的容积.二、拱桥问题
-
4. 北中环桥是省城太原的一座跨汾河大桥(如图1),它由五个高度不同,跨径也不同的抛物线型钢拱通过吊桥,拉锁与主梁相连,最高的钢拱如图2所示,此钢拱(近似看成二次函数的图象-抛物线)在同一竖直平面内,与拱脚所在的水平面相交于A,B两点,拱高为78米(即最高点O到AB的距离为78米),跨径为90米(即AB=90米),以最高点O为坐标原点,以平行于AB的直线为 轴建立平面直角坐标系,则此抛物线钢拱的函数表达式为( )
 A、 B、 C、 D、5. 如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为 ,两侧蹑地面 高处各有一盏灯,两灯间的水平距离为 ,则这个门洞的高度为 .(精确到 )
A、 B、 C、 D、5. 如图,有一个横截面边缘为抛物线的水泥门洞,门洞内的地面宽度为 ,两侧蹑地面 高处各有一盏灯,两灯间的水平距离为 ,则这个门洞的高度为 .(精确到 )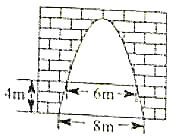 6. 如图,一座拱桥的轮廓是抛物线型,拱高6m,在长度为8m的两支柱OC和AB之间,还安装着三根支柱,相邻两支柱间的距离均为5m.
6. 如图,一座拱桥的轮廓是抛物线型,拱高6m,在长度为8m的两支柱OC和AB之间,还安装着三根支柱,相邻两支柱间的距离均为5m.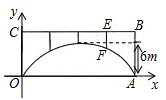 (1)、建立如图所示的直角坐标系,求拱桥抛物线的函数表达式;(2)、求支柱EF的长度;(3)、拱桥下面拟铺设行车道,要保证高3m的汽车能够通过(车顶与拱桥的距离不小于0.3m),行车道最宽可以铺设多少米?
(1)、建立如图所示的直角坐标系,求拱桥抛物线的函数表达式;(2)、求支柱EF的长度;(3)、拱桥下面拟铺设行车道,要保证高3m的汽车能够通过(车顶与拱桥的距离不小于0.3m),行车道最宽可以铺设多少米?三、抛球问题
-
7. 把一个物体以初速度v0(米/秒)竖直向上抛出,在不计空气阻力的情况下,物体的运动路线是一条抛物线,且物体的上升高度h(米)与抛出时间t(秒)之间满足:h=v0t- gt2(其中g是常数,取10米/秒2).某时,小明在距地面2米的O点,以10米/秒的初速度向上抛出一个小球,抛出2.1秒时,该小球距地面的高度是( )
A、1.05米 B、-1.05米 C、0.95米 D、-0.95米8. 为响应“足球进校园”的号召,我县教体局在今年 11 月份组织了“县长杯”校园足球比赛.在某场比赛中,一个球被从地面向上踢出,它距地面的高度 h(m)可用公式 h=﹣5t2+v0t 表示,其中 t(s)表示足球被踢出后经过的时间,v0(m/s)是足球被踢出时的速度,如果足球的最大高度到 20m,那么足球被踢出时的速度应达到m/s.9. 如图是一个倾斜角为a 的斜坡,将一个小球从斜坡的坡脚 O 点处抛出,落在 A点处,小球的运动路线可以用抛物线 来刻画,已知 tan a = .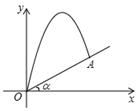 (1)、求抛物线表达式及点 A 的坐标.(2)、求小球在运动过程中离斜坡坡面 OA 的最大距离.
(1)、求抛物线表达式及点 A 的坐标.(2)、求小球在运动过程中离斜坡坡面 OA 的最大距离.四、销售问题
-
10. 某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足:y1=﹣x2+10x,y2=2x,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为( )A、30万元 B、40万元 C、45万元 D、46万元11. 某商户购进某种商品的进价是50元/个,根据市场调研发现售价是80元/个时,每月可卖出200个,若销售单价每降低1元,则每月可多卖出10个,同样若销售单价每增加1元,则每月可少卖出10个.若计划下月该商品的销售利润不低于5760元,则该商品的销售单价x(元)的取值范围是 .12. 一连锁店销售某品牌商品,该商品的进价是60元.因为是新店开业,所以连锁店决定当月前10天进行试营业活动,活动期间该商品的售价为每件80元,据调查研究发现:当天销售件数 (件)和时间第x(天)的关系式为 ( ),已知第4天销售件数是40件,第6天销售件数是44件.活动结束后,连锁店重新制定该商品的销售价格为每件100元,每天销售的件数也发生变化:当天销售数量 (件)与时间第x(天)的关系为: ( ).(1)、求 关于x的函数关系式;
(2)、若某天的日毛利润是1120元,求x的值;(3)、因为该连锁店是新店开业,所以试营业结束后,厂家给这个连锁店相应的优惠政策:当这个连锁店日销售量达到60件后(不含60),每多销售1件产品,当日销售的所有商品进价减少2元,设该店日销售量超过60件的毛利润总额为W,请直接写出W关于x的函数解析式,及自变量x的取值范围: .
五、求近似解
-
13. 二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表,则方程ax2+bx+c=0的一个解的范围是( )
x
6.17
6.18
6.19
y
-0.03
-0.01
0.02
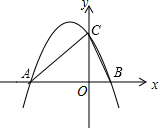
A、-0.03<x<-0.01 B、-0.01<x<0.02 C、6.18<x<6.19 D、6.17<x<6.1814. 如图,抛物线y=ax2和直线y=bx+c的两个交点坐标分别为A(-2,4),B(1,1), 则关于x的方程ax2=bx+c的解为.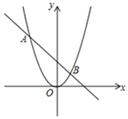
六、动态几何问题
-
15. 如图,在△ABC中,∠C=90°,AB=10cm,BC=8cm,点P从点A沿AC向点C以1cm/s的速度运动,同时点Q从点C沿CB向点B以2cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
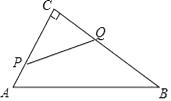 A、19cm2 B、16cm2 C、15cm2 D、12cm2
A、19cm2 B、16cm2 C、15cm2 D、12cm2