初中数学浙教版九年级上册1.3 二次函数的性质 强化提升训练
试卷更新日期:2019-08-22 类型:同步测试
一、综合训练
-
1. 如图窗户边框的上部分是由4个全等扇形组成的半圆,下部分是矩形,现在制作一个窗户边框的材料总长度为6米。(π取3)
 (1)、若设扇形半径为x,请用含x的代数式表示出AB。并求出x的取值范围。(2)、当x为何值时,窗户透光面积最大,最大面积为多少?(窗框厚度不予考虑)2. 在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-4的图象与x轴有两个公共点,m取满足条件的最小的整数·(1)、求此二次函数的解析式;(2)、当n≤x≤1时,函数值y的取值范围是一5≤y≤1-n,求n的值·3. 函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.(1)、分别求出当2≤x≤4时,三个函数:y=2x+1,y= ,y=2(x-1)2+1的最大值和最小值.
(1)、若设扇形半径为x,请用含x的代数式表示出AB。并求出x的取值范围。(2)、当x为何值时,窗户透光面积最大,最大面积为多少?(窗框厚度不予考虑)2. 在平面直角坐标系xOy中,二次函数y=mx2-(2m+1)x+m-4的图象与x轴有两个公共点,m取满足条件的最小的整数·(1)、求此二次函数的解析式;(2)、当n≤x≤1时,函数值y的取值范围是一5≤y≤1-n,求n的值·3. 函数学习中,自变量取值范围及相应的函数值范围问题是大家关注的重点之一,请解决下面的问题.(1)、分别求出当2≤x≤4时,三个函数:y=2x+1,y= ,y=2(x-1)2+1的最大值和最小值.
(2)、对于二次函数y=2(x-m)2+m-2,当2≤x≤4时有最小值为1,求m的值.
4. 汽车刹车后行驶的距离s(单位:米)关于行驶的时间t(单位:秒)的函数解析式是s=8t﹣2t2 , 汽车刹车后停下来前进的距离是米.5. 已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而减小,且-4≤x≤1时,y的最大值为7,则a的值为6. 如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们规定:当x取任意一个值时,x对应的函数值分别为y1和y2 , 若y1≠y2 , 取y1和y2中较小值为M;若y1=y2 , 记M=y1=y2 . ①当x>2时,M=y2;②当x<0时,M随x的增大而增大;③使得M大于4的x的值不存在;④若M=2,则x=1.上述结论正确的是(填写所有正确结论的序号).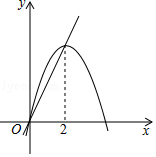 7. 在平面直角坐标系中,二次函数y=x2+2x-3的图象如图所示,点A(x1 , y1),B(x2 , y2)是该二次函数图象上的两点,其中-3≤x1<x2≤0,则下列结论正确的是( )
7. 在平面直角坐标系中,二次函数y=x2+2x-3的图象如图所示,点A(x1 , y1),B(x2 , y2)是该二次函数图象上的两点,其中-3≤x1<x2≤0,则下列结论正确的是( )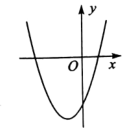
A、y1<y2 B、y1>y2 C、函数y的最小值是-3 D、函数y的最小值是-48. 在平面直角坐标系中,抛物线y=x2﹣2x+c(c为常数)的对称轴如图所示,且抛物线过点C(0,c). (1)、当c=﹣3时,点(x1 , y1)在抛物线y=x2﹣2x+c上,求y1的最小值;(2)、若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA= OB,求抛物线的解析式;(3)、当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.9. 已知二次函数y=ax2+bx+c(a≠0),过(1,y1)、(2,y2)。下列结论:
(1)、当c=﹣3时,点(x1 , y1)在抛物线y=x2﹣2x+c上,求y1的最小值;(2)、若抛物线与x轴有两个交点,自左向右分别为点A、B,且OA= OB,求抛物线的解析式;(3)、当﹣1<x<0时,抛物线与x轴有且只有一个公共点,求c的取值范围.9. 已知二次函数y=ax2+bx+c(a≠0),过(1,y1)、(2,y2)。下列结论:①若y1>0时,则a+b+c>0;
②若a=2b时,则y1<y2;
③若y1<0,y2>0,且a+b<0,则a>0。
其中正确的结论个数为( )
A、0个 B、1个 C、2个 D、3个二、中考演练
-
10. 已知抛物线y=2x2-4x+c与x轴有两个不同的交点.(1)、求c的取值范围;(2)、若抛物线y=2x2-4x+c经过点A(2,m)和点B(3,n),试比较m与n的大小,并说明理由.11. 已知抛物线y=ax2+bx+c(a≠0)的对称轴是直线x=1,其部分图象如图所示,下列说法中:①abc<0;②a﹣b+c<0;③3a+c=0;④当﹣1<x<3时,y>0,正确的是(填写序号).
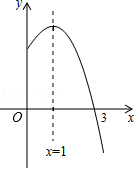 12. 已知二次函数y=x2﹣4x+k的图象的顶点在x轴下方,则实数k的取值范围是 .
12. 已知二次函数y=x2﹣4x+k的图象的顶点在x轴下方,则实数k的取值范围是 .
13. 如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中,错误的是( )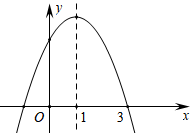 A、 B、 C、 D、14. 已知a,b是非零实数, ,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( )A、
A、 B、 C、 D、14. 已知a,b是非零实数, ,在同一平面直角坐标系中,二次函数y1=ax2+bx与一次函数y2=ax+b的大致图象不可能是( )A、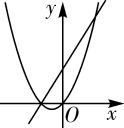 B、
B、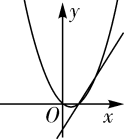 C、
C、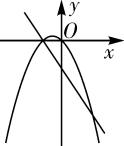 D、
D、 15. 抛物线 与坐标轴的交点个数为( )A、0 B、1 C、2 D、316. 在下列函数图象上任取不同两点 、 ,一定能使 成立的是( )A、 B、 C、 D、17. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、 的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线 C、当 时, 的值随 值的增大而增大,当 时, 的值随 值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到18. 二次函数 的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )
15. 抛物线 与坐标轴的交点个数为( )A、0 B、1 C、2 D、316. 在下列函数图象上任取不同两点 、 ,一定能使 成立的是( )A、 B、 C、 D、17. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、 的最小值为1 B、图象顶点坐标为(2,1),对称轴为直线 C、当 时, 的值随 值的增大而增大,当 时, 的值随 值的增大而减小 D、它的图象可以由 的图象向右平移2个单位长度,再向上平移1个单位长度得到18. 二次函数 的图象如图所示,对称轴是直线x=1.下列结论:①abc<0;②3a+c>0;③(a+c)2-b2<0;④a+b≤m(am+b)(m为实数).其中结论正确的个数为( )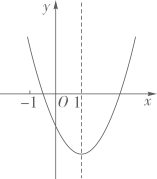 A、1 B、2个 C、3个 D、4个19. 已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4)(1)、求b,c满足的关系式(2)、设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式(3)、若该函数的图象不经过第三象限,当-5sx≤1时,函数的最大值与最小值之差为16,求b的值20. 设二次函数y=(x-x1)(x-x2)(x1 , x2是实数)。(1)、甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x= 时,y=- ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.(2)、写出二次函数图象的对称轴,并求该函数的最小值(用含x1 , x2的代数式表示).(3)、已知二次函数的图象经过(0,m)和(1,n)两点(m.n是实数)当0<x1<x2<1时,求证:0<mn< .
A、1 B、2个 C、3个 D、4个19. 已知函数y=x2+bx+c(b,c为常数)的图象经过点(-2,4)(1)、求b,c满足的关系式(2)、设该函数图象的顶点坐标是(m,n),当b的值变化时,求n关于m的函数解析式(3)、若该函数的图象不经过第三象限,当-5sx≤1时,函数的最大值与最小值之差为16,求b的值20. 设二次函数y=(x-x1)(x-x2)(x1 , x2是实数)。(1)、甲求得当x=0时,y=0;当x=1时,y=0;乙求得当x= 时,y=- ,若甲求得的结果都正确,你认为乙求得的结果正确吗?说明理由.(2)、写出二次函数图象的对称轴,并求该函数的最小值(用含x1 , x2的代数式表示).(3)、已知二次函数的图象经过(0,m)和(1,n)两点(m.n是实数)当0<x1<x2<1时,求证:0<mn< .