初中数学浙教版九年级上册1.2二次函数的图象(3) 同步训练
试卷更新日期:2019-08-22 类型:同步测试
一、基础夯实
-
1. 抛物线y=x2+x﹣1的对称轴是( )A、直线x=﹣1 B、直线x=1 C、直线x=﹣
 D、直线x=
D、直线x=  2. 用配方法求二次函数y=x2﹣10x+3的顶点坐标.3. 将抛物线y=x2﹣2x﹣3的图象先向右平移1个单位,再向下平移4个单位,所得图象的函数解析式为( )A、y=x2﹣3x﹣7 B、y=x2﹣x﹣7 C、y=x2﹣3x+1 D、y=x2﹣4x﹣44. 将二次函数y=﹣2x2+6x﹣4配成顶点式为( )A、
2. 用配方法求二次函数y=x2﹣10x+3的顶点坐标.3. 将抛物线y=x2﹣2x﹣3的图象先向右平移1个单位,再向下平移4个单位,所得图象的函数解析式为( )A、y=x2﹣3x﹣7 B、y=x2﹣x﹣7 C、y=x2﹣3x+1 D、y=x2﹣4x﹣44. 将二次函数y=﹣2x2+6x﹣4配成顶点式为( )A、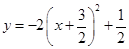 B、
B、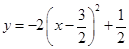 C、
C、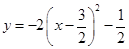 D、
D、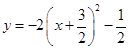 5. 已知二次函数y=﹣2x2 , y=﹣2(x﹣2)2 , y=﹣2(x﹣2)2+2,请回答下列问题:(1)、写出抛物线y=﹣2(x﹣2)2的顶点坐标,开口方向和对称轴;(2)、分别通过怎样的平移,可以由抛物线y=﹣2x2得到抛物线y=﹣2(x﹣2)2和y=﹣2(x﹣2)2+2?(3)、如果要得到抛物线y=﹣2(x﹣2017)2﹣2018,应将y=﹣2x2怎样平移?
5. 已知二次函数y=﹣2x2 , y=﹣2(x﹣2)2 , y=﹣2(x﹣2)2+2,请回答下列问题:(1)、写出抛物线y=﹣2(x﹣2)2的顶点坐标,开口方向和对称轴;(2)、分别通过怎样的平移,可以由抛物线y=﹣2x2得到抛物线y=﹣2(x﹣2)2和y=﹣2(x﹣2)2+2?(3)、如果要得到抛物线y=﹣2(x﹣2017)2﹣2018,应将y=﹣2x2怎样平移?二、提高特训
-
6. 已知抛物线y=﹣2x2+4x+1.
(1)、求这个抛物线的对称轴和顶点坐标;
(2)、将这个抛物线平移,使顶点移到点P(-2,0)的位置,写出所得新抛物线的表达式和平移的过程.
7. 将抛物线y=x2-4x+3平移,使它平移后图象的顶点为(-2,4),则需将该抛物线( )A、先向右移4个单位,再向上平移5个单位 B、先向右平移4个单位,再向下平移5个单位 C、先向左平移4个单位,再向上平移5个单位 D、先向左平移4个单位,再向下平移5个单位8. 二次函数 的图象是由 的图象向右平移1个单位,再向下平移2个单位得到的,则a= , b= , c= .9. 已知二次函数 的图像上部分点的坐标 满足下表:…
…
…
…
(1)、求这个二次函数的解析式;(2)、用配方法求出这个二次函数图象的顶点坐标和对称轴.10. 已知抛物线y=﹣x2+2x+2.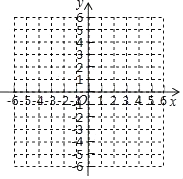 (1)、写出它的开口方向、对称轴和顶点坐标;(2)、在如图3的直角坐标系内画出y=﹣x2+2x+2的图象.11. 若二次函数y=ax2+bx+c的图象如图所示,则点(a+b,ac)在( )
(1)、写出它的开口方向、对称轴和顶点坐标;(2)、在如图3的直角坐标系内画出y=﹣x2+2x+2的图象.11. 若二次函数y=ax2+bx+c的图象如图所示,则点(a+b,ac)在( )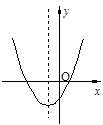 A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 抛物线y=ax2+2ax+c与x轴交于点A,B(点A在点B右边),且 ,求点A、B的坐标.13. 在同一平面直角坐标系中,一次函数y=kx-2k和二次函数y=-kx2+2x-4(k是常数且k≠0)的图象可能是( )
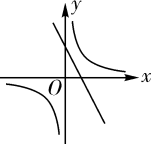
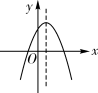
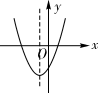
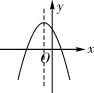
A、第一象限 B、第二象限 C、第三象限 D、第四象限12. 抛物线y=ax2+2ax+c与x轴交于点A,B(点A在点B右边),且 ,求点A、B的坐标.13. 在同一平面直角坐标系中,一次函数y=kx-2k和二次函数y=-kx2+2x-4(k是常数且k≠0)的图象可能是( )
A、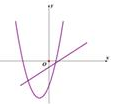 B、
B、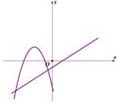 C、
C、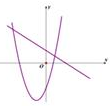 D、
D、
三、中考演练
-
14. 将抛物线 向上平移两个单位长度,再向右平移一个单位长度后,得到的抛物线解析式是( )A、 B、 C、 D、