初中数学浙教版九年级上册1.2二次函数的图象(2) 同步训练
试卷更新日期:2019-08-22 类型:同步测试
一、基础夯实
-
1. 抛物线 y=3(x+2)2﹣7 的对称轴是 .2. 抛物线 的顶点坐标是 .3. 对于抛物线 ,下列说法正确的是( )
A、开口向下,顶点坐标(5,3) B、开口向上,顶点坐标(5,3) C、开口向下,顶点坐标(-5,3) D、开口向上,顶点坐标(-5,3)4. 关于函数y=﹣(x+2)2﹣1的图象叙述正确的是( )A、开口向上 B、顶点(2,﹣1) C、与y轴交点为(0,﹣1) D、对称轴为直线x=﹣25. 二次函数y=(x+1)2 , 与x轴交点坐标为( )A、(—1,0) B、(1,0) C、(0,—1) D、(0,1)6. 如图是二次函数y=a(x+1)2+2的图象的一部分,根据图象回答下列问题: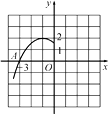 (1)、抛物线与x轴的一个交点A的坐标是 , 则抛物线与x轴的另一个交点B的坐标是;(2)、确定a的值;(3)、设抛物线的顶点是P,试求△PAB的面积.7. 请直接写出二次函数y=(x﹣1)2+2图象的开口方向、对称轴和顶点坐标.
(1)、抛物线与x轴的一个交点A的坐标是 , 则抛物线与x轴的另一个交点B的坐标是;(2)、确定a的值;(3)、设抛物线的顶点是P,试求△PAB的面积.7. 请直接写出二次函数y=(x﹣1)2+2图象的开口方向、对称轴和顶点坐标.
8. 抛物线y=2x2﹣1在y轴右侧的部分是(填“上升”或“下降”).9. 二次函数y=x2+1的图象大致是( )
A、 B、
B、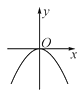 C、
C、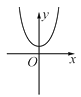 D、
D、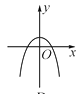 10. 函数 与 图像不同之处是( )
10. 函数 与 图像不同之处是( )
A、对称轴 B、开口方向 C、顶点 D、形状11. 如果要得到y=x2﹣6x+7的图象,需将y=x2的图象( )A、由向左平移3个单位,再向上平移2个单位 B、由向右平移3个单位,再向下平移2个单位 C、由向右平移3个单位,再向上平移2个单位 D、由向左平移3个单位,再向下平移2个单位二、提高特训
-
12. 把抛物线y=2(x﹣3)2+k向下平移1个单位长度后经过点(2,3),则k的值是( )A、2 B、1 C、0 D、﹣113. 用配方法把二次函数 化为 的形式,再指出该函数图象的开口方向、对称轴和顶点坐标.14. 如果点 , 在抛物线 上,那么 的值为;15. 飞机着陆后滑行的距离s(米)关于滑行的时间t(米)的函数解析式是s=90t﹣1.5t2 , 则飞机着陆后滑行到停止下来,滑行的距离为米.16. 若把函数y=(x-3)2-2的图象向左平移a个单位,再向上平移b个单位,所得图象的函数表达式是y=(x+3)2+2,则( )A、a=6,b=4 B、a=-6,b=4 C、a=6,b=-4 D、a=-6,b=-417. 已知,二次函数y=(x+2)2+k向左平移1个单位,再向下平移3个单位,得到二次函数y=(x+h)2﹣1,则h和k的值分别为( )A、3,﹣4 B、1,﹣4 C、1,2 D、3,218. 如图,已知A(0,2),B(2,2),C(-1,0),抛物线y=a(x-h)2+k过点C,顶点M位于第一象限且在线段AB的垂直平分线上,若抛物线与线段AB无公共点,则k的取值范围是( )
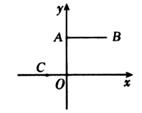 A、0<k<2 B、0<k<2或k> C、k> D、0<k<2或k>19. 已知二次函数 (a为常数),当a取不同的值时,其图象构成一个“抛物线系”.下图分别是当 时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是 .
A、0<k<2 B、0<k<2或k> C、k> D、0<k<2或k>19. 已知二次函数 (a为常数),当a取不同的值时,其图象构成一个“抛物线系”.下图分别是当 时二次函数的图象.它们的顶点在一条直线上,这条直线的解析式是 .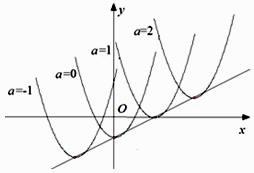 20. 已知函数 ,若使y=k成立的x值恰好有三个,则k的值为 .
20. 已知函数 ,若使y=k成立的x值恰好有三个,则k的值为 .
三、中考演练