初中数学浙教版九年级上册1.1 二次函数 同步训练
试卷更新日期:2019-08-22 类型:同步测试
一、基础夯实
-
1. 下列函数解析式中,一定为二次函数的是( )A、y=3x-1 B、y=ax2+bx+c C、s=2t2-2t+1 D、y=x2+
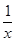 2. 下列函数关系中,不属于二次函数的是( )
2. 下列函数关系中,不属于二次函数的是( )
A、 B、 C、 D、3. 函数 ( 是常数)是二次函数的条件是( )
A、 B、 C、 D、4. 二次函数 的一次项系数是( )A、1 B、-1 C、2 D、-25. 已知点(-1,2)在二次函数y=ax2的图象上,那么a的值是( )
A、1 B、2 C、 D、-6. 已知关于x的二次函数y=3x2+2x+m+1的图象经过点(1,6),则m的值为.
7. 当m=时,函数 是二次函数.
8. 若 是关于x的二次函数,则a=9. 已知两个变量x,y之间的关系式为y=(a﹣2)x2+(b+2)x﹣3.(1)、当时,x,y之间是二次函数关系;
(2)、当时,x,y之间是一次函数关系.
二、提高特训
-
10. 下列各式中,y是x的二次函数的是( )A、xy+x2=2 B、x2﹣2y+2=0 C、y= D、y2﹣x=011. 二次函数的图象经过 三点,则它的解析式为( )A、 B、 C、 D、12. 在一个边长为2的正方形中挖去一个边长为x(0<x<2)的小正方形,如果设剩余部分的面积为y,那么y关于x的函数解析式是( )A、
 B、
B、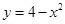 C、
C、 D、
D、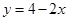 13. 喜迎圣诞,某商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.设每件商品的售价上涨x元(x正整数),每星期销售该商品的利润为y元,则y与x的函数解析式为( )A、y=﹣10x2+100x+2000 B、y=10x2+100x+2000 C、 y=﹣10x2+200x D、y=﹣10x2﹣100x+200014. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
13. 喜迎圣诞,某商店销售一种进价为50元/件的商品,售价为60元/件,每星期可卖出200件,若每件商品的售价每上涨1元,则每星期就会少卖出10件.设每件商品的售价上涨x元(x正整数),每星期销售该商品的利润为y元,则y与x的函数解析式为( )A、y=﹣10x2+100x+2000 B、y=10x2+100x+2000 C、 y=﹣10x2+200x D、y=﹣10x2﹣100x+200014. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )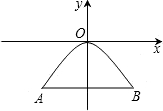 A、
A、 B、
B、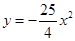 C、
C、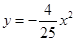 D、
D、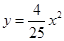 15. 平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如图所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为 ( )
15. 平时我们在跳绳时,绳摇到最高点处的形状可近似地看做抛物线,如图所示.正在摇绳的甲、乙两名同学拿绳的手间距为4 m,距地高均为1 m,学生丙、丁分别站在距甲拿绳的手水平距离1 m,2.5 m处.绳子在摇到最高处时刚好通过他们的头顶.已知学生丙的身高是1.5 m,则学生丁的身高为 ( )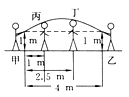 A、1.5 m B、1.625 m C、1.66 m D、1.67 m16. 如图,用一段长为40m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m,设AD的长为xm,菜园ABCD的面积为ym2 , 则函数y关于自变量x的函数关系式是 , x的取值范围是 .
A、1.5 m B、1.625 m C、1.66 m D、1.67 m16. 如图,用一段长为40m的篱笆围成一个一边靠墙的矩形菜园ABCD,墙长为18m,设AD的长为xm,菜园ABCD的面积为ym2 , 则函数y关于自变量x的函数关系式是 , x的取值范围是 . 17. 如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.
17. 如图,二次函数y=ax2+bx+c的图象与x轴交于A、B两点,其中A点坐标为(-1,0),点C(0,5),另抛物线经过点(1,8),M为它的顶点.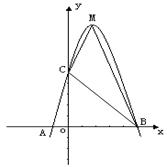 (1)、求抛物线的解析式(2)、求△MCB的面积S△MCB.18. 已知在直角坐标平面内,抛物线y=x2+bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C;(1)、求抛物线的表达式;(2)、求△ABC的面积.19. 根据下面的条件列出函数解析式,并判断列出的函数是否为二次函数:(1)、如果两个数中,一个比另一个大5,那么,这两个数的乘积p是较大的数m的函数;
(1)、求抛物线的解析式(2)、求△MCB的面积S△MCB.18. 已知在直角坐标平面内,抛物线y=x2+bx+6经过x轴上两点A,B,点B的坐标为(3,0),与y轴相交于点C;(1)、求抛物线的表达式;(2)、求△ABC的面积.19. 根据下面的条件列出函数解析式,并判断列出的函数是否为二次函数:(1)、如果两个数中,一个比另一个大5,那么,这两个数的乘积p是较大的数m的函数;
(2)、一个半径为10cm的圆上,挖掉4个大小相同的正方形孔,剩余的面积S(cm2)是方孔边长x(cm)的函数;
(3)、有一块长为60m、宽为40m的矩形绿地,计划在它的四周相同的宽度内种植阔叶草,中间种郁金香,那么郁金香的种植面积S(cm2)是草坪宽度a(m)的函数.