重庆市九校联盟2019届高三文数12月联合考试试卷
试卷更新日期:2019-08-22 类型:高考模拟
一、单选题
-
1. 若集合A={x|3-2x<-1},B={x|x(2x-5)≤0},则A∪B=( )A、 B、 C、[0,+∞) D、2. 若复数z满足(2+i)z=3-i,则z的虚部为( )A、1 B、-1 C、i D、-i3. 函数 的图象大致是( )A、
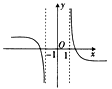 B、
B、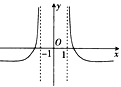 C、
C、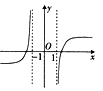 D、
D、 4. 已知平面向量 满足 ,且 ,则向量 的夹角 为( )A、 B、 C、 D、5. 已知函数f(x)为R上的奇函数,当x<0时, ,则xf(x)≥0的解集为( )A、[-1,0)∪[1,+∞) B、(-∞,-1]∪[1,+∞) C、[-1,0]∪[1,+∞) D、(-∞,-1]∪{0}∪[1,+∞)6. 设x , y满足约束条件 则z=4x+y的最小值为( )A、-3 B、-5 C、-14 D、-167. 某几何体的三视图如图所示(其中俯视图中的曲线是圆弧),则该几何体的表面积为( )
4. 已知平面向量 满足 ,且 ,则向量 的夹角 为( )A、 B、 C、 D、5. 已知函数f(x)为R上的奇函数,当x<0时, ,则xf(x)≥0的解集为( )A、[-1,0)∪[1,+∞) B、(-∞,-1]∪[1,+∞) C、[-1,0]∪[1,+∞) D、(-∞,-1]∪{0}∪[1,+∞)6. 设x , y满足约束条件 则z=4x+y的最小值为( )A、-3 B、-5 C、-14 D、-167. 某几何体的三视图如图所示(其中俯视图中的曲线是圆弧),则该几何体的表面积为( )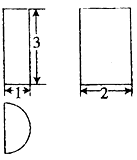 A、4π+6 B、6π+6 C、4π+3 D、6π+38. 为了得到y=−2cos 2x的图象,只需把函数 的图象( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度9. 已知双曲线 的左、右焦点分别为 , , 为 上一点, , 为坐标原点,若 ,则 ( )A、10 B、9 C、1 D、1或910. 如图,△ABC和△DEF均为等边三角形,AF=BD=CE , DF=2AF=20 cm,若在△ABC中随机投入260粒芝麻,则落在△DEF外的芝麻粒数约为( )
A、4π+6 B、6π+6 C、4π+3 D、6π+38. 为了得到y=−2cos 2x的图象,只需把函数 的图象( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度9. 已知双曲线 的左、右焦点分别为 , , 为 上一点, , 为坐标原点,若 ,则 ( )A、10 B、9 C、1 D、1或910. 如图,△ABC和△DEF均为等边三角形,AF=BD=CE , DF=2AF=20 cm,若在△ABC中随机投入260粒芝麻,则落在△DEF外的芝麻粒数约为( ) A、100 B、130 C、150 D、18011. 设0<m≤2,已知函数 ,对于任意x1 , x2∈[m-2,m],都有|f(x1)-f(x2)|≤1,则实数m的取值范围为( )A、 B、 C、 D、
A、100 B、130 C、150 D、18011. 设0<m≤2,已知函数 ,对于任意x1 , x2∈[m-2,m],都有|f(x1)-f(x2)|≤1,则实数m的取值范围为( )A、 B、 C、 D、二、填空题
-
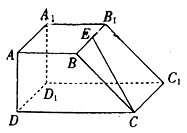
12. 已知函数 ,则 .13. 已知 , ,则cos 2α= .14. 如图,在直四棱柱ABCD-A1B1C1D1中,已知四边形ABCD是直角梯形,∠BAD=90°,AB∥CD , AB=AD=AA1=1,CD=2,E为BB1的中点,则直线AD与直线CE所成角的正切值为 .
 15. 点 在椭圆 上, 的右焦点为 ,点 在圆 上,则 的最小值为 .
15. 点 在椭圆 上, 的右焦点为 ,点 在圆 上,则 的最小值为 .三、解答题
-
16. 已知数列{an}的前n项和为Sn , a1=3,an+1=2Sn+3(n∈N*).(1)、求数列{an}的通项公式;(2)、设bn=log3an , 若数列 的前n项和为Tn , 证明:Tn<1.17. 2018年4月全国青少年足球超级联赛火爆开启,这是体育与教育的强强联手,这是培养足球运动员的黄金摇篮,也是全国青少年足球的盛宴.组委会在某场联赛结束后,随机抽取了300名观众进行对足球“喜爱度”的调查评分,将得到的分数分成6段:[64,70),[70,76),[76,82),[82,88),[88,94),[94,100]后得到如图所示的频率分布直方图.
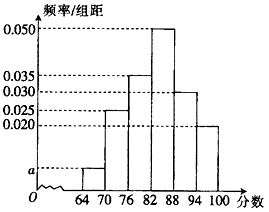 (1)、求a的值并估计这300名观众评分的中位数;(2)、若评分在“88分及以上”确定为“足球迷”,现从“足球迷”中按区间[88,94)与[94,100]两部分按分层抽样抽取5人,然后再从中任意选取两人作进一步的访谈,求这两人中至少有1人的评分在区间[94,100]的概率.18. 如图,在五面体ABCDFE中,底面ABCD为矩形,EF∥AB , BC⊥FD , 过BC的平面交棱FD于P , 交棱FA于Q .
(1)、求a的值并估计这300名观众评分的中位数;(2)、若评分在“88分及以上”确定为“足球迷”,现从“足球迷”中按区间[88,94)与[94,100]两部分按分层抽样抽取5人,然后再从中任意选取两人作进一步的访谈,求这两人中至少有1人的评分在区间[94,100]的概率.18. 如图,在五面体ABCDFE中,底面ABCD为矩形,EF∥AB , BC⊥FD , 过BC的平面交棱FD于P , 交棱FA于Q .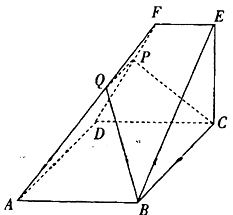 (1)、证明:PQ∥平面ABCD;(2)、若CD⊥BE , EF=EC=1, ,求五面体ABCDFE的体积.19. 已知抛物线y2=2px(p>0)的焦点为F , 过F且与x轴垂直的直线交该抛物线于A , B两点,|AB|=4.(1)、求抛物线的方程;(2)、过点F的直线l交抛物线于P , Q两点,若△OPQ的面积为4,求直线l的斜率(其中O为坐标原点).
(1)、证明:PQ∥平面ABCD;(2)、若CD⊥BE , EF=EC=1, ,求五面体ABCDFE的体积.19. 已知抛物线y2=2px(p>0)的焦点为F , 过F且与x轴垂直的直线交该抛物线于A , B两点,|AB|=4.(1)、求抛物线的方程;(2)、过点F的直线l交抛物线于P , Q两点,若△OPQ的面积为4,求直线l的斜率(其中O为坐标原点).