重庆市九校联盟2019届高三理数12月联合考试试卷
试卷更新日期:2019-08-22 类型:高考模拟
一、单选题
-
1. 若集合A={x|3-2x<1},B={x|4x-3x2≥0},则A∩B=( )A、(1,2] B、 C、[0,1) D、(1,+∞)2. 若复数z满足(2+i)z=3-i,则z的虚部为( )A、i B、-i C、1 D、-13. 已知 , ,则 ( )A、 B、 C、 D、4. 函数 的图象大致是( )A、
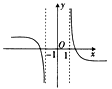 B、
B、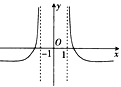 C、
C、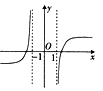 D、
D、 5. 已知单位向量 的夹角为 ,且 ,若向量m=2 -3 ,则|m|=( )A、9 B、10 C、3 D、6. 已知函数f(x)为R上的奇函数,当x<0时, ,则xf(x)≥0的解集为( )A、[-1,0)∪[1,+∞) B、(-∞,-1]∪[1,+∞) C、[-1,0]∪[1,+∞) D、(-∞,-1]∪{0}∪[1,+∞)7. 设x , y满足约束条件 则z=4x+y的最小值为( )A、-3 B、-5 C、-14 D、-168. 为了得到y=−2cos 2x的图象,只需把函数 的图象( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度9. 已知双曲线C: 的左、右焦点分别为F1 , F2 , P为C上一点, ,O为坐标原点,若|PF1|=10,则|OQ|=( )A、9 B、10 C、1 D、1或910. 的内角 的对边分别为 ,若 ,且 ,则 的面积的最大值是( )A、 B、 C、 D、411. 已知命题p:若x2+y2>2,则|x|>1或|y|>1;命题q:直线mx-2y-m-2=0与圆x2+y2-3x+3y+2=0必有两个不同交点,则下列说法正确的是( )A、¬p为真命题 B、p∧(¬q)为真命题 C、(¬p)∨q为假命题 D、(¬p)∨(¬q)为假命题12. 已知函数f(x)=e2x+ex+2-2e4 , g(x)=x2-3aex , 集合A={x|f(x)=0},B={x|g(x)=0},若存在x1∈A , x2∈B , 使得|x1-x2|<1,则实数a的取值范围为( )A、 B、 C、 D、
5. 已知单位向量 的夹角为 ,且 ,若向量m=2 -3 ,则|m|=( )A、9 B、10 C、3 D、6. 已知函数f(x)为R上的奇函数,当x<0时, ,则xf(x)≥0的解集为( )A、[-1,0)∪[1,+∞) B、(-∞,-1]∪[1,+∞) C、[-1,0]∪[1,+∞) D、(-∞,-1]∪{0}∪[1,+∞)7. 设x , y满足约束条件 则z=4x+y的最小值为( )A、-3 B、-5 C、-14 D、-168. 为了得到y=−2cos 2x的图象,只需把函数 的图象( )A、向左平移 个单位长度 B、向右平移 个单位长度 C、向左平移 个单位长度 D、向右平移 个单位长度9. 已知双曲线C: 的左、右焦点分别为F1 , F2 , P为C上一点, ,O为坐标原点,若|PF1|=10,则|OQ|=( )A、9 B、10 C、1 D、1或910. 的内角 的对边分别为 ,若 ,且 ,则 的面积的最大值是( )A、 B、 C、 D、411. 已知命题p:若x2+y2>2,则|x|>1或|y|>1;命题q:直线mx-2y-m-2=0与圆x2+y2-3x+3y+2=0必有两个不同交点,则下列说法正确的是( )A、¬p为真命题 B、p∧(¬q)为真命题 C、(¬p)∨q为假命题 D、(¬p)∨(¬q)为假命题12. 已知函数f(x)=e2x+ex+2-2e4 , g(x)=x2-3aex , 集合A={x|f(x)=0},B={x|g(x)=0},若存在x1∈A , x2∈B , 使得|x1-x2|<1,则实数a的取值范围为( )A、 B、 C、 D、二、填空题
-
13. 设命题p: ,tan x>0,则¬p为 .14. 已知函数 ,则 .15. 已知正数a , b满足3a+2b=1,则 的最小值为 .16. 已知F是抛物线y2=-16x的焦点,O为坐标原点,点P是抛物线准线上的一动点,点A在抛物线上,且|AF|=8,则|PA|+|PO|的最小值为 .
三、解答题
-
17. 已知数列{an}的前n项和为Sn , a1=3,an+1=2Sn+3(n∈N*).(1)、求数列{an}的通项公式;(2)、设bn=log3an , 若数列 的前n项和为Tn , 证明:Tn<1.18. 已知p:x2-(3+a)x+3a<0,其中a<3;q:x2+4x-5>0.(1)、若p是¬q的必要不充分条件,求实数a的取值范围;(2)、若p是q的充分不必要条件,求实数a的取值范围.19. 在△ABC中,内角A , B , C的对边分别是a , b , c , 且 .(1)、求角B的大小;(2)、求 的取值范围.20. 已知椭圆C: 的离心率为 ,且经过点 .(1)、求椭圆C的方程;(2)、直线l:y=kx+m(k>0,m2≠4)与椭圆C相交于A , B两点,若|AB|=4,试用m表示k .