湖南省湘西自治州四校2018-2019学年高二上学期文数12月联考试卷
试卷更新日期:2019-08-21 类型:月考试卷
一、单选题
-
1. 已知a,b,c∈R,下列说法正确的是( )A、a>b⇒ac2>bc2 B、 ⇒a>b C、a>b>0⇒ D、a>b⇒a2>b22. 在△ABC中, 所对的边为a,b,c,a=8,B=60°,A=45°,则b=( )A、 B、 C、 D、3. 椭圆 的右焦点到双曲线 的渐近线的距离是( )A、 B、 C、 D、4. 已知 是公差为1的等差数列, 为 的前 项和,则 ,则 ( )A、 B、12 C、 D、105. 函数 的定义域为开区间 ,其导函数 在 内的图象如图所示,则函数 在开区间 内极小值点的个数为( )
 A、1个 B、2个 C、3个 D、4个6. 下列说法正确的是( )A、命题“若 ,则 ”的否命题为“若 ,则 ”; B、命题“ ”的否定是“ ”; C、命题“若x=y,则 ”的逆否命题为真命题; D、“ ” 是“ ”的必要不充分条件.7. 已知变量 满足 ,则目标函数 有 ( )A、 B、 , 无最小值 C、 无最大值 D、 既无最大值,也无最小值8. 函数y= x2-ln x的单调递减区间为( )A、(0,1] B、(-1,1] C、[1,+∞) D、(0,+∞)9. 如图所示, , , 三点在地面上的同一直线上, ,从 两点测得 点的仰角分别为 , ,则 点离地面的高为 ( )
A、1个 B、2个 C、3个 D、4个6. 下列说法正确的是( )A、命题“若 ,则 ”的否命题为“若 ,则 ”; B、命题“ ”的否定是“ ”; C、命题“若x=y,则 ”的逆否命题为真命题; D、“ ” 是“ ”的必要不充分条件.7. 已知变量 满足 ,则目标函数 有 ( )A、 B、 , 无最小值 C、 无最大值 D、 既无最大值,也无最小值8. 函数y= x2-ln x的单调递减区间为( )A、(0,1] B、(-1,1] C、[1,+∞) D、(0,+∞)9. 如图所示, , , 三点在地面上的同一直线上, ,从 两点测得 点的仰角分别为 , ,则 点离地面的高为 ( )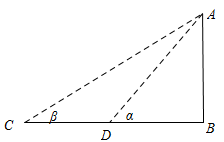 A、 B、 C、 D、10. 大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.是中华传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0、2、4、8、12、18、24、32、40、50…,则此数列第20项为( )A、128 B、162 C、180 D、20011. 点 是双曲线 : 与圆 : 的一个交点,且 ,其中 、 分别为 的左右焦点,则 的离心率为( )A、 B、 C、 D、12. 如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切).已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )
A、 B、 C、 D、10. 大衍数列,来源于《乾坤谱》中对易传“大衍之数五十”的推论.主要用于解释中国传统文化中的太极衍生原理.数列中的每一项,都代表太极衍生过程中,曾经经历过的两仪数量总和.是中华传统文化中隐藏着的世界数学史上第一道数列题.其前10项依次是0、2、4、8、12、18、24、32、40、50…,则此数列第20项为( )A、128 B、162 C、180 D、20011. 点 是双曲线 : 与圆 : 的一个交点,且 ,其中 、 分别为 的左右焦点,则 的离心率为( )A、 B、 C、 D、12. 如图,修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切).已知环湖弯曲路段为某三次函数图象的一部分,则该函数的解析式为( )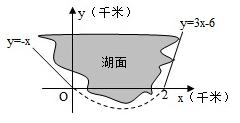 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 已知 ,则 取最小值是 .14. 如图,函数f(x)的图象是折线段ABC,其中A,B,C的坐标分别为(0,4),(2,0),(6,4),则 .
 15. 已知O为坐标原点,F为抛物线C: 的焦点,P为C上一点,若|PF|= ,则△POF的面积为 .16. 已知 , .对 , ,使 ,则 的取值范围 .
15. 已知O为坐标原点,F为抛物线C: 的焦点,P为C上一点,若|PF|= ,则△POF的面积为 .16. 已知 , .对 , ,使 ,则 的取值范围 .三、解答题
-
17. 已知命题p:方程 表示焦点在 轴上的椭圆,命题q:函数 在 上单调递减。若 为真, 为假,求m的取值范围.18. 已知不等式 的解集为 或 .
(I)求实数 的值;
(II)若正实数 、 满足 , ,求 的最小值.
19. 的内角A,B,C的对边分别别为a,b,c,已知(I)求 ;
(II)若 的面积为 ,求 的周长.