2016-2017学年河南省濮阳市濮阳县十校七年级下学期期中数学试卷
试卷更新日期：2017-06-23 类型：期中考试
一、选择题
-
1. 在平面直角坐标系中，点P（﹣2，﹣3）所在的象限是（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 9的平方根是（ ）
A、±3 B、± C、3 D、﹣33. 如图，直线a∥b，∠1=85°，∠2=30°，则∠3=（ ）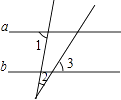
A、85° B、60° C、55° D、35°4. 如图，直线AB，CD相交于点O，射线OM平分∠AOC，ON⊥OM，若∠CON=55°，则∠AOM的度数为（ ）
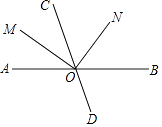A、35° B、45° C、55° D、65°5. 若|a﹣3|+ =0，则a+b的值是（ ）A、2 B、1 C、0 D、﹣16. 已知点P（0，m）在y轴的正半轴上，则点M（﹣m，﹣m﹣1）在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 若k﹣1＜ ＜k（k是整数），则k=（ ）A、7 B、8 C、9 D、108. 如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30°，那么这两个角是（ ）A、42°、138° B、都是10° C、42°、138°或42°、10° D、以上都不对二、填空题
-
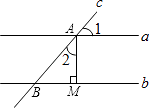
9. 4的算术平方根是；﹣27的立方根是 ．10. 写出一个大于3且小于4的无理数 ．11. 如图所示，直线a∥b，直线c与直线a，b分别相交于点A、点B，AM⊥b，垂足为M，若∠1=50°，则∠2= ．
12. 如图，AB∥CD，直线MN分别交AB、CD于点E，F，EG平分∠AEF，EG⊥FG于点G，若∠BEM=60°，则∠CFG= ．
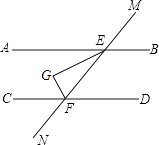13. 点C在x轴下方，y轴左侧，距离x轴4个单位长度，距离y轴3个单位长度，则点C的坐标为 ．14. 已知 =4.1，则 = ．15. 小明、小亮、小刚、小颖一起研究一道数学题，如图，已知EF⊥AB，CD⊥AB，小明说：“如果还知道∠CDG=∠BFE，则能得到∠AGD=∠ACB．”
小亮说：“把小明的已知和结论倒过来，即由∠AGD=∠ACB，
可得到∠CDG=∠BFE．”
小刚说：“∠AGD一定大于∠BFE．”
小颖说：“如果连接GF，则GF一定平行于AB．”
他们四人中，有个人的说法是正确的．
三、解答题
-
16. 计算： +|﹣2|+ +（﹣1）2016 ．17. 已知 =3，3a+b﹣1的平方根是±4，c是 的整数部分，求a+2b+c的算术平方根．18.
如图，△AOB中，A、B两点的坐标分别为（2，5），（6，2），把△AOB向下平移3个单位，向左平移2个单位，得到△CDE．
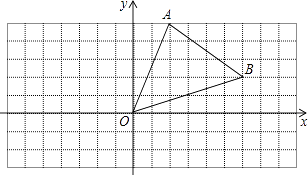(1)、写出C、D、E三点的坐标，并在图中画出△CDE．(2)、求出△CDE的面积．19. 如图，若直线AB与直线CD交于点O，OA平分∠COF，OE⊥CD．
(1)、写出图中与∠EOB互余的角；(2)、若∠AOF=30°，求∠BOE和∠DOF的度数．20. 如图，已知直线AB、CD被直线EF所截，FG平分∠EFD，∠1=∠2=80°，求∠BGF的度数．解：因为∠1=∠2=80°（已知），
所以AB∥CD（）
所以∠BGF+∠3=180°（）
因为∠2+∠EFD=180°（邻补角的性质）．
所以∠EFD= ． （等式性质）．
因为FG平分∠EFD（已知）．
所以∠3=∠EFD（角平分线的性质）．
所以∠3= ． （等式性质）．
所以∠BGF= ． （等式性质）．
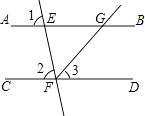21. 已知：如图，∠1=∠C，∠3=∠4，求证：∠2=∠D．
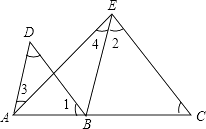22.在平面直角坐标系中，一蚂蚁从原点O出发，按向上、向右、向下、向右的方向依次不断移动，每次移动1个单位，其行走路线如图所示．
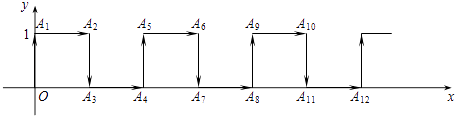(1)、填写下列各点的坐标：A4 ， A8；(2)、写出点A4n的坐标（n为正整数）；(3)、蚂蚁从点A2014到点A2017的移动方向 ．23. 问题情境：如图1，AB∥CD，∠PAB=130°，∠PCD=120°，求∠APC的度数．小明的思路是：过P作PE∥AB，通过平行线性质来求∠APC．
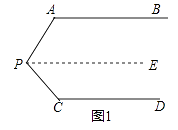(1)、按小明的思路，易求得∠APC的度数为度；(2)、问题迁移：如图2，AB∥CD，点P在射线OM上运动，记∠PAB=α，∠PCD=β，当点P在B、D两点之间运动时，问∠APC与α、β之间有何数量关系？请说明理由；
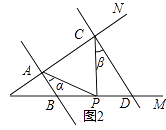(3)、在（2）的条件下，如果点P在B、D两点外侧运动时（点P与点O、B、D三点不重合），请直接写出∠APC与α、β之间的数量关系．