2016-2017学年河北省保定市定州市七年级下学期期中数学试卷
试卷更新日期：2017-06-23 类型：期中考试
一、选择题
-
1. 点A的坐标是（﹣2，5），则点A在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 如图，下列说法不正确的是（ ）
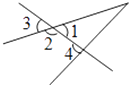A、∠1和∠2是同旁内角 B、∠1和∠3是对顶角 C、∠3和∠4是同位角 D、∠1和∠4是内错角3. 实数﹣2，0.3， ， ， ﹣π中，无理数的个数是（ ）A、2 B、3 C、4 D、54. 化简 的结果是（ ）A、5 B、﹣5 C、±5 D、255. 如图，数轴上点P表示的数可能是（ ）
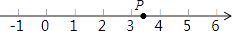A、 B、 C、 D、6. 已知A（2，﹣5），AB平行于y轴，则点B的坐标可能是（ ）A、（﹣2，5） B、（2，6） C、（5，﹣5） D、（﹣5，5）7. 若x使（x﹣1）2=4成立，则x的值是（ ）A、3 B、﹣1 C、3或﹣1 D、±28. 如图，已知∠1=∠2，∠3=80°，则∠4=（ ）
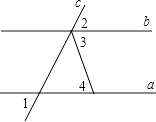A、50° B、60° C、70° D、80°9. 若平面直角坐标系内的点M在第四象限，且M到x轴的距离为1，到y轴的距离为2，则点M的坐标为（ ）A、（2，1） B、（﹣2，1） C、（2，﹣1） D、（1，﹣2）10. 如图，AB∥CD，DE⊥CE，∠1=34°，则∠DCE的度数为（ ）
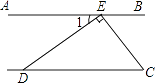A、34° B、56° C、66° D、54°11. 下列说法正确的是（ ）①0是绝对值最小的实数；
②相反数大于本身的数是负数；
③数轴上原点两侧的数互为相反数；
④带根号的数是无理数．
A、①② B、①③ C、①②③ D、①②③④12. 如图是某公园里一处矩形风景欣赏区ABCD，长AB=50米，宽BC=25米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那小明沿着小路的中间，从出口A到出口B所走的路线（图中虚线）长为（ ）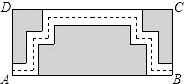
A、100米 B、99米 C、98米 D、74米二、填空题
-
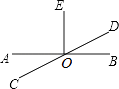
13. ﹣4是的立方根．14. 若点P（m+3，m+1）在x轴上，则点P的坐标为 ．15. A、B两点的坐标分别为（1，0）、（0，2），若将线段AB平移至A1B1 ， 点A1、B1的坐标分别为（2，a），（b，3），则a+b=16. 如图，AB、CD相交于O，OE⊥AB，若∠EOD=65°，则∠AOC= ．
17. 如图是某植物园的平面图，图中A馆所在地用坐标表示为（1，0），B馆所在地用坐标表示为（﹣3，﹣1），那么C馆所在地用坐标表示为 ．
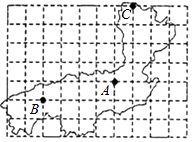18. 有一个数值转换器，原理如下：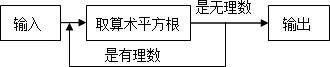
当输入的数是16时，则输出的数是 ．
三、解答题
-
19. 计算。(1)、计算： ﹣4 +(2)、计算： ﹣ +（ ）2+|1﹣ |20. 已知2x﹣y的算术平方根为4，﹣2是y的立方根，求﹣2xy的平方根．21.
如图，已知A（﹣1，0），B（1，1），把线段AB平移，使点B移动到点D（3，4）处，这时点A移动到点C处．
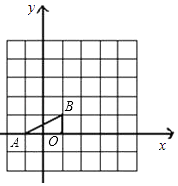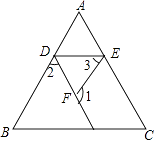
(1)、画出平移后的线段CD，并写出点C的坐标；(2)、如果平移时只能左右或者上下移动，叙述线段AB是怎样移到CD的．22. 在横线上填写理由，完成下面的证明．如图，已知∠1+∠2=180°，∠B=∠3，求证∠C=∠AED
证明：∵∠1+∠2=180°（已知），∠1+∠DFE=180°（）
∴∠2=∠DFE（）
∴AB∥EF（）
∴∠3=∠ADE（）
又∵∠B=∠3（已知）
∴∠B=∠ADE（）
∴DE∥BC（）
∴∠C=∠AED（）
23. 如图，直线AB∥CD，BC平分∠ABD，∠1=65°，求∠2的度数．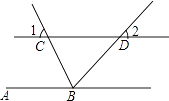
24. 已知：OA⊥OC，∠AOB：∠AOC=2：3，画出图形，并求∠BOC的度数．25. 阅读下面的文字，解答问题：大家知道 是无理数，而无理数是无限不循环小数，因此 的小数部分我们不可能全部地写出来，于是小明用 ﹣1来表示 的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为 的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵22＜（ ）2＜32 ， 即2＜ ＜3，∴ 的整数部分为2，小数部分为（ ﹣2）．请解答：
(1)、 的整数部分是 ， 小数部分是(2)、如果 的小数部分为a， 的整数部分为b，求a+b﹣ 的值．26. 如图，A（﹣1，0），C（1，4），点B在x轴上，且AB=3．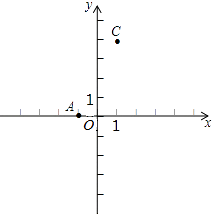
(1)、求点B的坐标；(2)、求△ABC的面积；(3)、在y轴上是否存在点P，使以A、B、P三点为顶点的三角形的面积为10？若存在，请直接写出点P的坐标；若不存在，请说明理由．