2017年山东省济宁市中考数学试卷
试卷更新日期:2017-06-23 类型:中考真卷
一、选择题
-
1. 的倒数是( )A、6 B、﹣6 C、 D、﹣2. 单项式9xmy3与单项式4x2yn是同类项,则m+n的值是( )A、2 B、3 C、4 D、53. 下列图形中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 4. 某桑蚕丝的直径约为0.000016米,将0.000016用科学记数法表示是( )A、1.6×10﹣4 B、1.6×10﹣5 C、1.6×10﹣6 D、16×10﹣45. 下列几何体中,主视图、俯视图、左视图都相同的是( )A、
4. 某桑蚕丝的直径约为0.000016米,将0.000016用科学记数法表示是( )A、1.6×10﹣4 B、1.6×10﹣5 C、1.6×10﹣6 D、16×10﹣45. 下列几何体中,主视图、俯视图、左视图都相同的是( )A、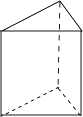 B、
B、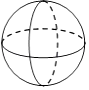 C、
C、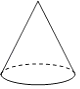 D、
D、 6. 若 + +1在实数范围内有意义,则x满足的条件是( )A、x≥ B、x≤ C、x= D、x≠7. 计算(a2)3+a2•a3﹣a2÷a﹣3 , 结果是( )A、2a5﹣a B、2a5﹣ C、a5 D、a68. 将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,不放回;再随机摸出一球,两次摸出的球上的汉字组成“孔孟”的概率是( )A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为 ,则图中阴影部分的面积是( )
6. 若 + +1在实数范围内有意义,则x满足的条件是( )A、x≥ B、x≤ C、x= D、x≠7. 计算(a2)3+a2•a3﹣a2÷a﹣3 , 结果是( )A、2a5﹣a B、2a5﹣ C、a5 D、a68. 将分别标有“孔”“孟”“之”“乡”汉字的四个小球装在一个不透明的口袋中,这些球除汉字外无其他差别,每次摸球前先搅拌均匀,随机摸出一球,不放回;再随机摸出一球,两次摸出的球上的汉字组成“孔孟”的概率是( )A、 B、 C、 D、9. 如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,将Rt△ABC绕点A逆时针旋转30°后得到Rt△ADE,点B经过的路径为 ,则图中阴影部分的面积是( )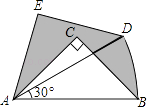 A、 B、 C、 ﹣ D、10.
A、 B、 C、 ﹣ D、10.如图,A,B是半径为1的⊙O上两点,且OA⊥OB,点P从点A出发,在⊙O上以每秒一个单位长度的速度匀速运动,回到点A运动结束,设运动时间为x(单位:s),弦BP的长为y,那么下列图象中可能表示y与x函数关系的是( )
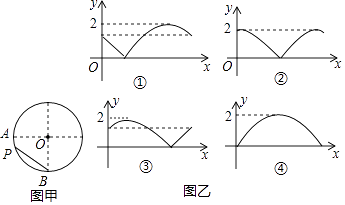 A、① B、③ C、②或④ D、①或③
A、① B、③ C、②或④ D、①或③二、填空题
-
11. 分解因式:ma2+2mab+mb2=.12. 请写出一个过点(1,1),且与x轴无交点的函数解析式:.13. 《孙子算经》是中国古代重要的数学著作,其中有一段文字的大意是:甲、乙两人各有若干钱,如果甲得到乙所有钱的一半,那么甲共有钱48文;如果乙得到甲所有钱的 ,那么乙也共有钱48文,甲、乙两人原来各有多少钱?设甲原有x文钱,乙原有y文钱,可列方程组是.14. 如图,在平面直角坐标系中,以O为圆心,适当长为半径画弧,交x轴于点M,交y轴于点N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧在第二象限内交于点P(a,b),则a与b的数量关系是.
 15. 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2 , 如此继续下去,则正六边形A4B4C4D4E4F4的面积是.
15. 如图,正六边形A1B1C1D1E1F1的边长为1,它的六条对角线又围成一个正六边形A2B2C2D2E2F2 , 如此继续下去,则正六边形A4B4C4D4E4F4的面积是.
三、解答题
-
16. 解方程: =1﹣ .17. 为了参加学校举行的传统文化知识竞赛,某班进行了四次模拟训练,将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图:
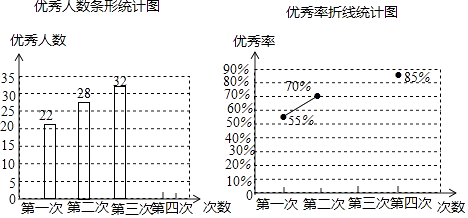
请根据以上两图解答下列问题:
(1)、该班总人数是;(2)、根据计算,请你补全两个统计图;(3)、观察补全后的统计图,写出一条你发现的结论.18. 某商店经销一种双肩包,已知这种双肩包的成本价为每个30元.市场调查发现,这种双肩包每天的销售量y(单位:个)与销售单价x(单位:元)有如下关系:y=﹣x+60(30≤x≤60).设这种双肩包每天的销售利润为w元.
(1)、求w与x之间的函数解析式;(2)、这种双肩包销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?(3)、如果物价部门规定这种双肩包的销售单价不高于48元,该商店销售这种双肩包每天要获得200元的销售利润,销售单价应定为多少元?19. 如图,已知⊙O的直径AB=12,弦AC=10,D是 的中点,过点D作DE⊥AC,交AC的延长线于点E. (1)、求证:DE是⊙O的切线;(2)、求AE的长.20. 实验探究:(1)、如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(1)、求证:DE是⊙O的切线;(2)、求AE的长.20. 实验探究:(1)、如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论. (2)、将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.
(2)、将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.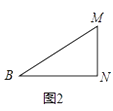 21. 已知函数y=mx2﹣(2m﹣5)x+m﹣2的图象与x轴有两个公共点.(1)、求m的取值范围,并写出当m取范围内最大整数时函数的解析式;(2)、题(1)中求得的函数记为C1 ,
21. 已知函数y=mx2﹣(2m﹣5)x+m﹣2的图象与x轴有两个公共点.(1)、求m的取值范围,并写出当m取范围内最大整数时函数的解析式;(2)、题(1)中求得的函数记为C1 ,①当n≤x≤﹣1时,y的取值范围是1≤y≤﹣3n,求n的值;
②函数C2:y=m(x﹣h)2+k的图象由函数C1的图象平移得到,其顶点P落在以原点为圆心,半径为 的圆内或圆上,设函数C1的图象顶点为M,求点P与点M距离最大时函数C2的解析式.
22.定义:点P是△ABC内部或边上的点(顶点除外),在△PAB,△PBC,△PCA中,若至少有一个三角形与△ABC相似,则称点P是△ABC的自相似点.
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P是△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线y= (x>0)上的任意一点,点N是x轴正半轴上的任意一点.
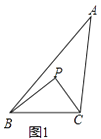 (1)、
(1)、如图2,点P是OM上一点,∠ONP=∠M,试说明点P是△MON的自相似点;当点M的坐标是( ,3),点N的坐标是( ,0)时,求点P的坐标;
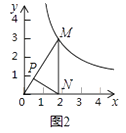 (2)、
(2)、如图3,当点M的坐标是(3, ),点N的坐标是(2,0)时,求△MON的自相似点的坐标;
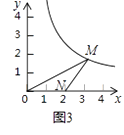 (3)、是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.
(3)、是否存在点M和点N,使△MON无自相似点?若存在,请直接写出这两点的坐标;若不存在,请说明理由.