2017年山东省德州市中考数学试卷

试卷更新日期：2017-06-23 类型：中考真卷

进入出卷网下载

一、选择题

1. ﹣2的倒数是（）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、﹣2 D、2

查看试题解析
2. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 2016年，我市“全面改薄”和解决大班额工程成绩突出，两项工程累计开工面积达477万平方米，各项指标均居全省前列，477万用科学记数法表示正确的是（）

A、4.77×10⁵ B、47.7×10⁵ C、4.77×10⁶ D、0.477×10⁶

查看试题解析
4. 如图，两个等直径圆柱构成如图所示的T型管道，则其俯视图正确的是（）

A、 B、 C、 D、

查看试题解析
5. 下列运算正确的是（）

A、（a²）^m=a^2m B、（2a）³=2a³ C、a³•a^﹣⁵=a^﹣¹⁵ D、a³÷a^﹣⁵=a^﹣²

查看试题解析
6. 某专卖店专营某品牌的衬衫，店主对上一周中不同尺码的衬衫销售情况统计如下：
尺码
39
40
41
42
43
平均每天销售数量/件
10
12
20
12
12
该店主决定本周进货时，增加了一些41码的衬衫，影响该店主决策的统计量是（）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
7. 下列函数中，对于任意实数x₁ ， x₂ ，当x₁＞x₂时，满足y₁＜y₂的是（）

A、y=﹣3x+2 B、y=2x+1 C、y=2x²+1 D、y=﹣ $\frac{1}{x}$

查看试题解析
8. 不等式组 ${\begin{matrix} 2 x + 9 \geq 3 \\ \frac{1 + 2 x}{3} > x - 1 \end{matrix}$ 的解集是（）

A、x≥﹣3 B、﹣3≤x＜4 C、﹣3≤x＜2 D、x＞4

查看试题解析
9. 公式L=L₀+KP表示当重力为P时的物体作用在弹簧上时弹簧的长度，L₀代表弹簧的初始长度，用厘米（cm）表示，K表示单位重力物体作用在弹簧上时弹簧拉伸的长度，用厘米（cm）表示．下面给出的四个公式中，表明这是一个短而硬的弹簧的是（）

A、L=10+0.5P B、L=10+5P C、L=80+0.5P D、L=80+5P

查看试题解析
10. 某校美术社团为练习素描，他们第一次用120元买了若干本资料，第二次用240元在同一商家买同样的资料，这次商家每本优惠4元，结果比上次多买了20本，求第一次买了多少本资料？若设第一次买了x本资料，列方程正确的是（）

A、 $\frac{240}{x - 20}$ ﹣ $\frac{120}{x}$ =4 B、 $\frac{240}{x + 20}$ ﹣ $\frac{120}{x}$ =4 C、 $\frac{120}{x}$ ﹣ $\frac{240}{x - 20}$ =4 D、 $\frac{120}{x}$ ﹣ $\frac{240}{x + 20}$ =4

查看试题解析
11.
如图放置的两个正方形，大正方形ABCD边长为a，小正方形CEFG边长为b（a＞b），M在BC边上，且BM=b，连接AM，MF，MF交CG于点P，将△ABM绕点A旋转至△ADN，将△MEF绕点F旋转至△NGF，给出以下五个结论：①∠MAD=∠AND；②CP=b﹣ $\frac{b^{2}}{a}$ ；③△ABM≌△NGF；④S_四边形_AMFN=a²+b²；⑤A，M，P，D四点共圆，其中正确的个数是（）

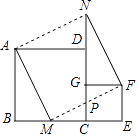A、2 B、3 C、4 D、5

查看试题解析
12. 观察下列图形，它是把一个三角形分别连接这个三角形三边的中点，构成4个小三角形，挖去中间的一个小三角形（如图1）；对剩下的三个小三角形再分别重复以上做法，…将这种做法继续下去（如图2，图3…），则图6中挖去三角形的个数为（）

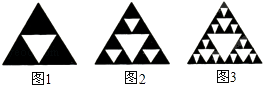A、121 B、362 C、364 D、729

查看试题解析

二、填空题

13. 计算： $\sqrt{8}$ ﹣ $\sqrt{2}$ = ．

查看试题解析
14. 如图是利用直尺和三角板过已知直线l外一点P作直线l的平行线的方法，其理由是．

查看试题解析
15. 方程3x（x﹣1）=2（x﹣1）的解为．

查看试题解析
16. 淘淘和丽丽是非常要好的九年级学生，在5月分进行的物理、化学、生物实验技能考试中，考试科目要求三选一，并且采取抽签方式取得，那么他们两人都抽到物理实验的概率是．

查看试题解析
17. 某景区修建一栋复古建筑，其窗户设计如图所示．圆O的圆心与矩形ABCD对角线的交点重合，且圆与矩形上下两边相切（E为上切点），与左右两边相交（F，G为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m，根据设计要求，若∠EOF=45°，则此窗户的透光率（透光区域与矩形窗面的面积的比值）为．

查看试题解析

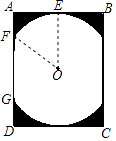
三、解答题

18. 先化简，再求值： $\frac{a^{2} - 4 a + 4}{a^{2} - 4}$ ÷ $\frac{a - 2}{a^{2} + 2 a}$ ﹣3，其中a= $\frac{7}{2}$ ．

查看试题解析
19. 随着移动终端设备的升级换代，手机已经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况（选项：A．和同学亲友聊天；B．学习；C．购物；D．游戏；E．其它），端午节后某中学在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：
选项
频数
频率
A
10
m
B
n
0.2
C
5
0.1
D
p
0.4
E
5
0.1
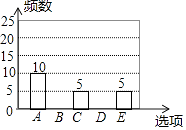
根据以上信息解答下列问题：

(1)、这次被调查的学生有多少人？

(2)、求表中m，n，p的值，并补全条形统计图．

(3)、若该中学约有800名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调查结果，就中学生如何合理使用手机给出你的一条建议．

查看试题解析
20. 如图，已知Rt△ABC，∠C=90°，D为BC的中点，以AC为直径的⊙O交AB于点E．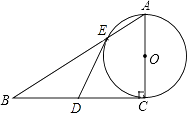

(1)、求证：DE是⊙O的切线；

(2)、若AE：EB=1：2，BC=6，求AE的长．

查看试题解析
21. 如图所示，某公路检测中心在一事故多发地段安装了一个测速仪器，检测点设在距离公路10m的A处，测得一辆汽车从B处行驶到C处所用时间为0.9秒，已知∠B=30°，∠C=45°．

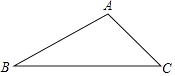(1)、求B，C之间的距离；（保留根号）

(2)、如果此地限速为80km/h，那么这辆汽车是否超速？请说明理由．（参考数据： $\sqrt{3}$ ≈1.7， $\sqrt{2}$ ≈1.4）

查看试题解析
22. 随着新农村的建设和旧城的改造，我们的家园越来越美丽，小明家附近广场中央新修了个圆形喷水池，在水池中心竖直安装了一根高为2米的喷水管，它喷出的抛物线形水柱在与水池中心的水平距离为1米处达到最高，水柱落地处离池中心3米．

(1)、请你建立适当的平面直角坐标系，并求出水柱抛物线的函数解析式；

(2)、求出水柱的最大高度的多少？

查看试题解析
23.
如图1，在矩形纸片ABCD中，AB=3cm，AD=5cm，折叠纸片使B点落在边AD上的E处，折痕为PQ，过点E作EF∥AB交PQ于F，连接BF．

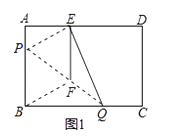(1)、求证：四边形BFEP为菱形；

(2)、
当点E在AD边上移动时，折痕的端点P、Q也随之移动；
①当点Q与点C重合时（如图2），求菱形BFEP的边长；
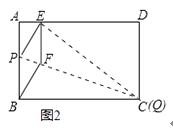
②若限定P、Q分别在边BA、BC上移动，求出点E在边AD上移动的最大距离．

查看试题解析
24.
有这样一个问题：探究同一平面直角坐标系中系数互为倒数的正、反比例函数y= $\frac{1}{k}$ x与y= $\frac{k}{x}$ （k≠0）的图象性质．
小明根据学习函数的经验，对函数y= $\frac{1}{k}$ x与y= $\frac{k}{x}$ ，当k＞0时的图象性质进行了探究．
下面是小明的探究过程：

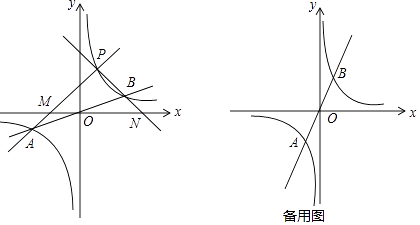(1)、如图所示，设函数y= $\frac{1}{k}$ x与y= $\frac{k}{x}$ 图象的交点为A，B，已知A点的坐标为（﹣k，﹣1），则B点的坐标为；

(2)、若点P为第一象限内双曲线上不同于点B的任意一点．
①设直线PA交x轴于点M，直线PB交x轴于点N．求证：PM=PN．
证明过程如下，设P（m， $\frac{k}{m}$ ），直线PA的解析式为y=ax+b（a≠0）．
则 ${\begin{matrix} - k a + b = - 1 \\ m a + b = \frac{k}{m} \end{matrix}$ ，
解得 ${\begin{cases} ａ＝（） \\ ｂ＝（） \end{cases}$
∴直线PA的解析式为 $\underline{}$
请你把上面的解答过程补充完整，并完成剩余的证明．
②当P点坐标为（1，k）（k≠1）时，判断△PAB的形状，并用k表示出△PAB的面积．

查看试题解析

尺码	39	40	41	42	43
平均每天销售数量/件	10	12	20	12	12

选项	频数	频率
A	10	m
B	n	0.2
C	5	0.1
D	p	0.4
E	5	0.1