浙江省金丽衢十二校2019届高三数学第一次联考试卷

试卷更新日期：2019-08-19 类型：高考模拟

进入出卷网下载

一、单选题

1. 若集合 $A = (- \infty ， 5)$ ， $B = [3 ， + \infty)$ ，则 $(C_{R} A) \cup^{} (C_{R} B) =$ （）

A、 $R$ B、 $\emptyset$ C、 $[3 ， 5)$ D、 $(- \infty ， 3) \cup^{} [5 ， + \infty)$

查看试题解析
2. 已知向量 $\overset{⇀}{a} = (4 ， \sqrt{3})$ ， $\overset{⇀}{b} = (1 ， 5 \sqrt{3})$ ，则 $\overset{⇀}{a}$ 与 $\overset{⇀}{b}$ 的夹角为（）

A、 $30 °$ B、 $45 °$ C、 $60 °$ D、 $90 °$

查看试题解析
3. 等比数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，已知 $S_{2} = 3$ ， $S_{4} = 15$ ，则 $S_{3} =$ （）

A、7 B、-9 C、7或-9 D、 $\frac{63}{8}$

查看试题解析
4. 双曲线 $9 y^{2} - 4 x^{2} = 1$ 的渐近线方程为（）

A、 $y = \pm \frac{4}{9} x$ B、 $y = \pm \frac{9}{4} x$ C、 $y = \pm \frac{2}{3} x$ D、 $y = \pm \frac{3}{2} x$

查看试题解析
5. 已知一个几何体的三视图如图所示，则该几何体的体积为（）

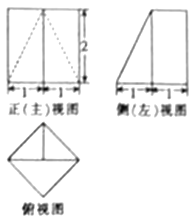A、 $\frac{32}{3}$ B、 $\frac{16}{3}$ C、 $\frac{8}{3}$ D、 $\frac{4}{3}$

查看试题解析
6. 已知复数 $z$ 满足 $z i^{5} = {(π + 3 i)}^{2}$ ，则 $\bar{z}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
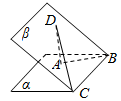7. 如图，二面角 $α - B C - β$ 的大小为 $\frac{π}{6}$ ， $A B \subset α$ ， $C D \subset β$ ，且 $A B = \sqrt{2}$ ， $B C = C D = 2$ ， $∠ A B C = \frac{π}{4} ， ∠ B C D = \frac{π}{3}$ ，则 $A D$ 与 $β$ 所成角的大小为（）

A、 $\frac{π}{4}$ B、 $\frac{π}{3}$ C、 $\frac{π}{6}$ D、 $\frac{π}{12}$

查看试题解析
8. 五人进行过关游戏，每人随机出现左路和右路两种选择．若选择同一条路的人数超过2人，则他们每人得1分；若选择同一条路的人数小于3人，则他们每人得0分，记小强游戏得分为 $ξ$ ，则 $E ξ =$ （）

A、 $\frac{5}{16}$ B、 $\frac{11}{16}$ C、 $\frac{5}{8}$ D、 $\frac{1}{2}$

查看试题解析

二、填空题

9. 已知 $n \in N^{*}$ ， ${(x^{2} - \frac{1}{\sqrt{5} x^{3}})}^{n}$ 的展开式中存在常数项，则 $n$ 的最小值为，此时常数项为．

查看试题解析
10. 偶函数 $f (x)$ 满足 $f (x - 1) = f (x + 1)$ ，且当 $x \in [0 ， 1]$ 时， $f (x) = x$ ，则 $f (\frac{4}{3}) =$ ，则若在区间 $[- 1 ， 3]$ 内，函数 $g (x) = f (x) - k x - k$ 有4个零点，则实数 $k$ 的取值范围是．

查看试题解析
11. 若实数 $x$ 、 $y$ 满足 $x > y > 0$ ，且 ${log}_{2} x + {log}_{2} y = 1$ ，则 $\frac{2}{x} + \frac{1}{y}$ 的最小值是， $\frac{x - y}{x^{2} + y^{2}}$ 的最大值为．

查看试题解析
12. 在从100到999的所有三位数中，百位、十位、个位数字依次构成等差数列的有个；构成等比数列的有个．

查看试题解析
13. 若等边 $Δ A B C$ 的边长为 $2 \sqrt{3}$ ，平面内一点 $M$ 满足 $\vec{C M} = \frac{1}{6} \vec{C B} + \frac{2}{3} \vec{C A}$ ，则 $\vec{M A} • \vec{M B} =$

查看试题解析
14. 已知函数 $y = sin x + \sqrt{3} cos x$ 是由 $y = sin x - \sqrt{3} cos x$ 向左平移 $φ (φ \in (0 ， 2 π))$ 个单位得到的，则 $φ =$ ．

查看试题解析
15. 已知 $P$ 是椭圈 $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 上的动点，过 $P$ 作椭圆的切线 $l$ 与 $x$ 轴、 $y$ 轴分别交于点 $A$ 、 $B$ ，当 $Δ A O B$ （ $O$ 为坐标原点）的面积最小时， $cos ∠ F_{1} P F_{2} = \frac{3}{4}$ （ $F_{1}$ 、 $F_{2}$ 是椭圆的两个焦点），则该椭圆的离心率为．

查看试题解析

三、解答题

16. 如图，在 $Δ A B C$ 中，已知点 $D$ 在边 $A B$ 上， $A D = 3 D B$ ， $cos A = \frac{4}{5}$ ， $cos ∠ A C B = \frac{5}{13}$ ， $B C = 13$ ．

(1)、求 $cos B$ 的值；

(2)、求 $C D$ 的长.

查看试题解析
17. 如图，在四棱锥P－ABCD中，已知PA⊥平面ABCD ，且四边形ABCD为直角梯形，∠ABC＝∠BAD＝ $\frac{π}{2}$ ，PA＝AD＝2，AB＝BC＝1，点M、E分别是PA、PD的中点

(1)、求证：CE//平面BMD

(2)、点Q为线段BP中点，求直线PA与平面CEQ所成角的余弦值.

查看试题解析
18. 已知数列 ${a_{n}}$ ， $a_{1} = 2$ ， $a_{2} = 6$ ，且满足 $\frac{a_{n + 1} + a_{n - 1}}{a_{n} + 1} = 2$ （ $n \geq 2$ 且 $n \in N^{*}$ ）

(1)、求证： ${a_{n + 1} - a_{n}}$ 为等差数列；

(2)、令 $b_{n} = \frac{10 (n + 1)}{a_{n}} - \frac{1}{2}$ ，设数列 ${b_{n}}$ 的前 $n$ 项和为 $S_{n}$ ，求 ${S_{2 n} - S_{n}}$ 的最大值.

查看试题解析
19. 已知椭圆 $C ： \frac{x^{2}}{2} + y^{2} = 1$ 左顶点为 $A$ ， $O$ 为原点， $M$ ， $N$ 是直线 $x = t$ 上的两个动点，且 $M O ⊥ O N$ ，直线 $A M$ 和 $A N$ 分别与椭圆 $C$ 交于 $E$ ， $D$ 两点

(1)、若 $t = - 1$ ，求 $Δ M O N$ 的面积的最小值；

(2)、若 $E$ ， $O$ ， $D$ 三点共线，求实数 $t$ 的值.

查看试题解析
20. 已知函数 $f (x) = - x^{3} + 9 x^{2} - 26 x + 27$ ．

(1)、若 $f (x)$ 在 $x = x_{1} ， x_{2} (x_{1} \neq x_{2})$ 处导数相等，证明： $f (x_{1}) + f (x_{2})$ 为定值，并求出该定值；

(2)、已知对于任意 $k > 0$ ，直线 $y = k x + a$ 与曲线 $y = f (x)$ 有唯一公共点，求实数 $a$ 的取值范围.

查看试题解析