新疆乌鲁木齐市2019届高三理数第二次诊断性测试试卷
试卷更新日期:2019-08-19 类型:高考模拟
一、单选题
-
1. 集合 , ,则 ( )A、 B、 C、 D、2. 设 是虚数单位,则复数 ( )A、 B、 C、 D、3. 若变量x,y满足约束条件 ,则 的最大值是( )A、0 B、2 C、5 D、64. 执行如图所示程序框图的输出结果是( )
 A、3 B、5 C、7 D、95. 设 , 是两条不同的直线, , 是两个不同的平面,则下列命题正确的是( )A、若 , ,则 B、若 , ,则 C、若 , , , ,则 D、若 , , ,则6. 已知等差数列 的公差不为零,且 , , 成等比数列,则 ( )A、 B、 C、 D、7. 设 ,则 的大小关系为( )A、 B、 C、 D、8. 已知椭圆 的焦点分别为 , ,点 , 在椭圆上, 于 , , ,则椭圆方程为( )A、 B、 C、 D、9. 函数 的图象大致为( )A、
A、3 B、5 C、7 D、95. 设 , 是两条不同的直线, , 是两个不同的平面,则下列命题正确的是( )A、若 , ,则 B、若 , ,则 C、若 , , , ,则 D、若 , , ,则6. 已知等差数列 的公差不为零,且 , , 成等比数列,则 ( )A、 B、 C、 D、7. 设 ,则 的大小关系为( )A、 B、 C、 D、8. 已知椭圆 的焦点分别为 , ,点 , 在椭圆上, 于 , , ,则椭圆方程为( )A、 B、 C、 D、9. 函数 的图象大致为( )A、 B、
B、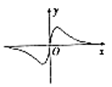 C、
C、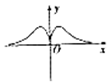 D、
D、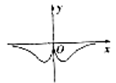 10. 已知函数 的最小正周期为 ,且 ,则 的最小值为( )A、 B、 C、 D、11. 我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金杖,长5尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”设该金杖由粗到细是均匀变化的,其重量为 ,现将该金杖截成长度相等的10段,记第 段的重量为 ,且 ,若 ,则 ( )A、4 B、5 C、6 D、712. 如图,是棱长为1的正方体的平面展开图,则在这个正方体中,以下结论正确的是( )
10. 已知函数 的最小正周期为 ,且 ,则 的最小值为( )A、 B、 C、 D、11. 我国古代数学著作《九章算术》有如下问题:“今有金箠,长五尺,斩本一尺,重四斤,斩末一尺,重二斤,问次一尺各重几何?”意思是:“现有一根金杖,长5尺,一头粗,一头细,在粗的一端截下1尺,重4斤;在细的一端截下1尺,重2斤;问依次每一尺各重多少斤?”设该金杖由粗到细是均匀变化的,其重量为 ,现将该金杖截成长度相等的10段,记第 段的重量为 ,且 ,若 ,则 ( )A、4 B、5 C、6 D、712. 如图,是棱长为1的正方体的平面展开图,则在这个正方体中,以下结论正确的是( ) A、点 到 的距离为 B、三棱锥 的体积是 C、 与平面 所成的角是 D、 与 所成的角是
A、点 到 的距离为 B、三棱锥 的体积是 C、 与平面 所成的角是 D、 与 所成的角是二、填空题
-
13. 有5名学生做志愿者服务,将他们分配到图书馆、科技馆、养老院这三个地方去服务,每个地方至少有1名学生,则不同的分配方案有种(用数字作答).14. 已知 是双曲线 的焦点,过 作一条渐近线的平行线与另一条渐近线交于 点,若 ( 是坐标原点)的面积为1,则双曲线的方程为 .15. 已知 , ,则 .16. 已知 , 是函数 (其中常数 )图象上的两个动点,点 ,若 的最小值为0,则函数 的最大值为 .
三、解答题
-
17. 在 中,角 的对边分别为 ,已知 , ,(1)、若 ,求 ;(2)、求 的面积 的最大值.18. 如图,在四棱锥 中,底面 是菱形, 平面 ,且 ,点 , 分别是 和 的中点.

(Ⅰ)求证 平面 ;
(Ⅱ)求二面角 的余弦值.
19. 某学校高二年级的第二学期,因某学科的任课教师王老师调动工作,于是更换了另一名教师赵老师继任.第二学期结束后从全学年的该门课的学生考试成绩中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如下: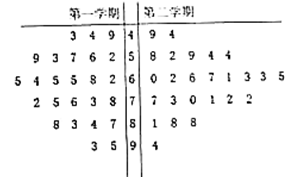
学校秉持均衡发展、素质教育的办学理念,对教师的教学成绩实行绩效考核,绩效考核方案规定:每个学期的学生成绩中与其中位数相差在 范围内(含 )的为合格,此时相应的给教师赋分为1分;与中位数之差大于10的为优秀,此时相应的给教师赋分为2分;与中位数之差小于-10的为不合格,此时相应的给教师赋分为-1分.
(Ⅰ)问王老师和赵老师的教学绩效考核成绩的期望值哪个大?
(Ⅱ)是否有 的把握认为“学生成绩取得优秀与更换老师有关”.
附:
0.050
0.010
0.001
3.841
6.635
10.828